2012 : WHAT IS YOUR FAVORITE DEEP, ELEGANT, OR BEAUTIFUL EXPLANATION?

Genes, Claustrum, and Consciousness 

What's my favorite elegant idea? The elucidation of DNA's structure is surely the most obvious, but it bears repeating. I'll argue that the same strategy used to crack the genetic code might prove successful in cracking the "neural code" of consciousness and self. It's a long shot, but worth considering.

The ability to grasp analogies, and seeing the difference between deep and superficial ones, is a hallmark of many great scientists; Francis Crick and James Watson were no exception. Crick himself cautioned against the pursuit of elegance in biology, given that evolution proceeds happenstantially—"God is a hacker," he famously said, adding (according to my colleague Don Hoffman), "Many a young biologist has slit his own throat with Ockham's razor." Yet his own solution to the riddle of heredity ranks with natural selection as biology's most elegant discovery. Will a solution of similar elegance emerge for the problem of consciousness?

It is well known that Crick and Watson unraveled the double helical structure of the DNA molecule: two twisting complementary strands of nucleotides. Less well known is the chain of events culminating in this discovery.

First, Mendel's laws dictated that genes are particulate (a first approximation still held to be accurate). Then Thomas Morgan showed that fruit flies zapped with x-rays became mutants with punctate changes in their chromosomes, yielding the clear conclusion that the chromosomes are where the action is. Chromosomes are composed of histones and DNA; as early as 1928, the British bacteriologist Fred Griffith showed that a harmless species of bacterium, upon incubation with a heat-killed virulent species, actually changes into the virulent species! This was almost as startling as a pig walking into a room with a sheep and two sheep emerging. Later, Oswald Avery showed that DNA was the transformative principle here. In biology, knowledge of structure often leads to knowledge of function—one need look no further than the whole of medical history. Inspired by Griffith and Avery, Crick and Watson realized that the answer to the problem of heredity lay in the structure of DNA. Localization was critical, as, indeed, it may prove to be for brain function.

Crick and Watson didn't just describe DNA's structure, they explained its significance. They saw the analogy between the complementarity of molecular strands and the complementarity of parent and offspring—why pigs beget pigs and not sheep. At that moment modern biology was born.

I believe there are similar correlations between brain structure and mind function, between neurons and consciousness. I am stating the obvious here only because there are some philosophers, called "new mysterians," who believe the opposite. The erudite Colin McGinn has written, for instance, "The brain is only tangentially relevant to consciousness." (There are many philosophers who would disagree, e.g., Churchland, Dennett, and Searle.)

After his triumph with heredity, Crick turned to what he called the "second great riddle" in biology—consciousness. There were many skeptics. I remember a seminar Crick was giving on consciousness at the Salk Institute here in La Jolla. He'd barely started when a gentleman in attendance raised a hand and said, "But Doctor Crick, you haven't even bothered to define the word consciousness before embarking on this." Crick's response was memorable: "I'd remind you that there was never a time in the history of biology when a bunch of us sat around the table and said, 'Let's first define what we mean by life.' We just went out there and discovered what it was—a double helix. We leave matters of semantic hygiene to you philosophers."

Crick did not, in my opinion, succeed in solving consciousness (whatever that might mean). Nonetheless, I believe he was headed in the right direction. He had been richly rewarded earlier in his career for grasping the analogy between biological complementarities, the notion that the structural logic of the molecule dictates the functional logic of heredity. Given his phenomenal success using the strategy of structure-function analogy, it is hardly surprising that he imported the same style of thinking to study consciousness. He and his colleague Christoff Koch did so by focusing on a relatively obscure structure called the claustrum.

The claustrum is a thin sheet of cells underlying the insular cortex of the brain, one on each hemisphere. It is histologically more homogeneous than most brain structures, and intriguingly, unlike most brain structures (which send and receive signals to and from a small subset of other structures), the claustrum is reciprocally connected with almost every cortical region. The structural and functional streamlining might ensure that, when waves of information come through the claustrum, its neurons will be exquisitely sensitive to the timing of the inputs.

What does this have to do with consciousness? Instead of focusing on pedantic philosophical issues, Crick and Koch began with their naïve intuitions. "Consciousness" has many attributes—continuity in time, a sense of agency or free will, recursiveness or "self-awareness," etc. But one attribute that stands out is subjective unity: you experience all your diverse sense impressions, thoughts, willed actions and memories as being a unity—not jittery or fragmented. This attribute of consciousness, with the accompanying sense of the immediate "present" or "here and now," is so obvious that we don't usually think about it; we regard it as axiomatic.

So a central feature of consciousness is its unity—and here is a brain structure that sends and receives signals to and from practically all other brain structures, including the right parietal (involved in polysensory convergence and embodiment) and anterior cingulate (involved in the experience of "free will"). Thus the claustrum seems to unify everything anatomically, and consciousness does so mentally. Crick and Koch recognized that this may not be a coincidence: the claustrum may be central to consciousness; indeed it may embody the idea of the " Cartesian theater" that's taboo among philosophers—or is at least the conductor of the orchestra. This is this kind of childlike reasoning that often leads to great discoveries. Obviously, such analogies don't replace rigorous science, but they're a good place to start. Crick and Koch may be right or wrong, but their idea is elegant. If they're right, they've paved the way to solving one of the great mysteries of biology. Even if they're wrong, students entering the field would do well to emulate their style. Crick has been right too often to ignore.

I visited him at his home in La Jolla in July of 2004. He saw me to the door as I was leaving and as we parted, gave me a sly, conspiratorial wink: "I think it's the claustrum, Rama; it's where the secret is." A week later he passed away. 

Boscovich's Explanation Of Atomic Forces

A great example how a great deal of amazing insight can be gained from some very simple considerations is the explanation of atomic forces by the 18th century Jesuit polymath Roger Boscovich, who was born in Dubrovnik.

One of the great philosophical arguments at the time took place between the adherents of Descartes who—following Aristotle—thought that forces can only be the result of immediate contact and those who followed Newton and believed in his concept of force acting at a distance. Newton was the revolutionary here, but his opponents argued—with some justification—that "action at a distance" brought back into physics "occult" explanations that do not follow from the "clear and distinct" understanding that Descartes demanded. (In the following I am paraphrasing reference works.) Boscovich, a forceful advocate of the Newtonian point of view, turned the question around: Let's understand exactly what happens during the interaction that we would call immediate contact?

His arguments are very easy to understand and extremely convincing. Let's imagine two bodies, one of which is traveling at a speed of, say, 6 units, the other at a speed of 12 with the faster body catching up with the slower one along the same straight path. We imagine what transpires when the two bodies collide. By conservation of the "quantity of motion," both bodies should continue after collision along the same path, each with a speed of 9 units (in the case of inelastic collision, or in case of elastic collision for a brief period right after the collision)

But how did the velocity of the faster body come to be reduced from 12 to 9, and that of the slower body increased from 6 to 9? Clearly, the time interval for the change in velocities cannot be zero, for then, argued Boscovich, the instantaneous change in speed would violate the law of continuity. Furthermore, we would have to say that at the moment of impact, the speed of one body is simultaneously 12 and 9, which is patently absurd.

It is therefore necessary for the change in speed to take place in a small, yet finite, amount of time. But with this assumption, we arrive at yet another contradiction. Suppose, for example, that after a small interval of time, the speed of the faster body is 11, and that of the slower body is 7. But this would mean that they are not moving at the same velocity, and the front surface of the faster body would advance through the rear surface of the slower body, which is impossible because we have assumed that the bodies are impenetrable. It therefore becomes apparent that the interaction must take place immediately before the impact of the two bodies and that this interaction can only be a repulsive one because it is expressed in the slowing down of one body and the speeding up of the other.

Moreover, this argument is valid for arbitrary speeds, so one can no longer speak of definite dimensions for the particles that were until now thought of as impenetrable, namely, for the atoms. An atom should rather be viewed as a point source of force, with the force emanating from it acting in some complicated fashion that depends on distance.

According to Boscovich, when bodies are far apart, they act on each other through a force corresponding to the gravitational force, which is inversely proportional to the square of the distance. But with decreasing distance, this law must be modified because, in accordance with the above considerations, the force changes sign and must become a repulsive force. Boscovich even plotted fanciful traces of how the force should vary with distance in which the force changed sign several times, hinting to the existence of minima in the potential and the existence of stable bonds between the particles—the atoms.

With this idea Boscovich not only offered a new picture for interactions in place of the Aristotelian-Cartesian theory based on immediate contact, but also presaged our understanding of the structure of matter, especially that of solid bodies.

Sexual Conflict Theory

A fascinating parallel has occurred in the history of the traditionally separate disciplines of evolutionary biology and psychology. Biologists historically viewed reproduction as an inherently cooperative venture. A male and female would couple for the shared goal of reproduction of mutual offspring. In psychology, romantic harmony was presumed to be the normal state. Major conflicts within romantic couples were and still are typically seen as signs of dysfunction. A radical reformulation embodied by sexual conflict theory changes these views.

Sexual conflict occurs whenever the reproductive interests of an individual male and individual female diverge, or more precisely when the "interests" of genes inhabiting individual male and female interactants diverge. Sexual conflict theory defines the many circumstances in which discord is predictable and entirely expected.

Consider deception on the mating market. If a man is pursuing a short-term mating strategy and the woman for whom he has sexual interest is pursuing a long-term mating strategy, conflict between these interactants is virtually inevitable. Men are known to feign long-term commitment, interest, or emotional involvement for the goal of casual sex, interfering with women's long-term mating strategy. Men's have evolved sophisticated strategies of sexual exploitation. Conversely, women sometimes present themselves as costless sexual opportunities, and then intercalate themselves into a man's mating mind to such a profound degree that he wakes up one morning and suddenly realizes that he can't live without her—one version of the ‘bait and switch' tactic in women's evolved arsenal.

Once coupled in a long-term romantic union, a man and a woman often still diverge in their evolutionary interests. A sexual infidelity by the woman might benefit her by securing superior genes for her progeny, an event that comes with catastrophic costs to her hapless partner who unknowingly devotes resources to a rival's child. From a woman's perspective, a man's infidelity risks the diversion of precious resources to rival women and their children. It poses the danger of losing the man's commitment entirely. Sexual infidelity, emotional infidelity, and resource infidelity are such common sources of sexual conflict that theorists have coined distinct phrases for each.

But all is not lost. As evolutionist Helena Cronin has eloquently noted, sexual conflict arises in the context of sexual cooperation. The evolutionary conditions for sexual cooperation are well-specified: When relationships are entirely monogamous; when there is zero probability of infidelity or defection; when the couple produces offspring together, the shared vehicles of their genetic cargo; and when joint resources cannot be differentially channeled, such as to one set of in-laws versus another.

These conditions are sometimes met, leading to great love and harmony between a man and a woman. The prevalence of deception, sexual coercion, stalking, intimate partner violence, murder, and the many forms of infidelity reveal that conflict between the sexes is ubiquitous. Sexual conflict theory, a logical consequence of modern evolutionary genetics, provides the most beautiful theoretical explanation for these darker sides of human sexual interaction.

A Hot Young Earth: Unquestionably Beautiful and Stunningly Wrong

Around 4.567 billion years ago, a giant cloud of dust collapsed in on itself. At the center of the cloud our Sun began to burn, while the outlying dust grains began to stick together as they orbited the new star. Within a million years, those clumps of dust had become protoplanets. Within about 50 million years, our own planet had already reached about half its current size. As more protoplanets crashed into Earth, it continued to grow. All told, it may have taken another fifty million years to reach its full size—a time during which a Mars-sized planet crashed into it, leaving behind a token of its visit: our Moon.

The formation of the Earth commands our greatest powers of imagination. It is primordially magnificent. But elegant is not the word I'd use to describe the explanation I just sketched out. Scientists did not derive it from first principles. There is no equivalent of E=mc² that predicts how the complex violence of the early Solar System produced a watery planet that could support life.

In fact, the only reason that we now know so much about how the Earth formed is because geologists freed themselves from a seductively elegant explanation that was foisted on them 150 years ago. It was unquestionably beautiful, and stunningly wrong.

The explanation was the work of one of the greatest physicists of the nineteenth century, William Thompson (a k a Lord Kelvin). Kelvin's accomplishments ranged from the concrete (figuring out how to lay a telegraph cable from Europe to America) to the abstract (the first and second laws of thermodynamics). Kelvin spent much of his career writing equations that could let him calculate how fast hot things got cold. Kelvin realized that he could use these equations to estimate how old the Earth is. "The mathematical theory on which these estimates are founded is very simple," Kelvin declared when he unveiled it in 1862.

At the time, scientists generally agreed that the Earth had started out as a ball of molten rock and had been cooling ever since. Such a birth would explain why rocks are hot at the bottom of mine shafts: the surface of the Earth was the first part to cool, and ever since, the remaining heat inside the planet has been flowing out into space. Kelvin reasoned that over time, the planet should steadily grow cooler. He used his equations to calculate how long it should take for a molten sphere of rock to cool to Earth's current temperature, with its observed rate of heat flow. His verdict was a brief 98 million years.

Geologists howled in protest. They didn't know how old the Earth was, but they thought in billions of years, not millions. Charles Darwin—who was a geologist first and then a biologist later—estimated that it had taken 300 million years for a valley in England to erode into its current shape. The Earth itself, Darwin argued, was far older. And later, when Darwin published his theory of evolution, he took it for granted that the Earth was inconceivably old. That luxury of time provided room for evolution to work slowly and imperceptibly.

Kelvin didn't care. His explanation was so elegant, so beautiful, so simple that it had to be right. It didn't matter how much trouble it caused for other scientists who would ignore thermodynamics. In fact, Kelvin made even more trouble for geologists when he took another look at his equations. He decided his first estimate had been too generous. The Earth might be only 10 million years old.

It turned out that Kelvin was wrong, but not because his equations were ugly or inelegant. They were flawless. The problem lay in the model of the Earth to which Kelvins applied his equations.

The story of Kelvin's refutation got a bit garbled in later years. Many people (myself included) have mistakenly claimed that his error stemmed from his ignorance of radioactivity. Radioactivity was only discovered in the early 1900s as physicists worked out quantum physics. The physicist Ernst Rutherford declared that the heat released as radioactive atom broke down inside the Earth kept it warmer than it would be otherwise. Thus a hot Earth did not have to be a young Earth.

It's true that radioactivity does give off heat, but there isn't enough inside the planet is to account for the heat flowing out of it. Instead, Kelvin's real mistake was assuming that the Earth was just a solid ball of rock. In reality, the rock flows like syrup, its heat lifting it up towards the crust, where it cools and then sinks back into the depths once more. This stirring of the Earth is what causes earthquakes, drives old crust down into the depths of the planet, and creates fresh crust at ocean ridges. It also drives heat up into the crust at a much greater rate than Kelvin envisioned.

That's not to say that radioactivity didn't have its own part to play in showing that Kelvin was wrong. Physicists realized that the tick-tock of radioactive decay created a clock that they could use to estimate the age of rocks with exquisite precision. Thus we can now say that the Earth is not just billions of years old, but 4.567 billion.

Elegance unquestionably plays a big part in the advancement of science. The mathematical simplicity of quantum physics is lovely to behold. But in the hands of geologists, quantum physics has brought to light the glorious, messy, and very inelegant history of our planet. 

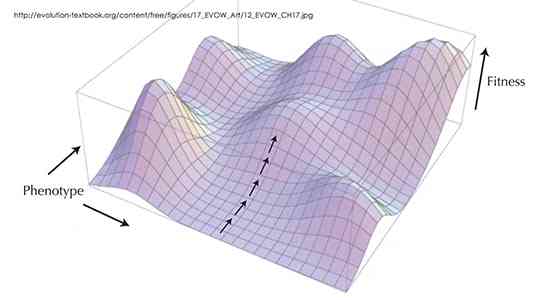
Fitness Landscapes

The first time I saw a fitness landscape cartoon (in Garrett Hardin's Man And Nature, 1969), I knew it was giving me advice on how not to get stuck over-adapted—hence overspecialized—on some local peak of fitness, when whole mountain ranges of opportunity could be glimpsed in the distance, but getting to them involved venturing "downhill" into regions of lower fitness. I learned to distrust optimality.

Fitness landscapes (sometimes called "adaptive landscapes") keep turning up when people try to figure out how evolution or innovation works in a complex world. An important critique by Marvin Minsky and Seymour Papert of early optimism about artificial intelligence warned that seemingly intelligent agents would dumbly "hill climb" to local peaks of illusory optimality and get stuck there. Complexity theorist Stuart Kauffman used fitness landscapes to visualize his ideas about the "adjacent possible" in 1993 and 2000, and that led in turn to Steven Johnson's celebration of how the "adjacent possible" works for innovation in Where Good Ideas Come From.

The man behind the genius of fitness landscapes was the founding theorist of population genetics, Sewell Wright (1889-1988). In 1932 he came up with the landscape as a way to visualize and explain how biological populations escape the potential trap of a local peak by imagining what might drive their evolutionary "path" downhill from the peak toward other possibilities. Consider these six diagrams of his :

[Image credit: © Sewall Wright, The Role of Mutation, Inbreeding, Crossbreeding, and Selection in Evolution, Sixth International Congress of Genetics, Brooklyn, NY: Brooklyn Botanical Garden, 1932.]

The first two illustrate how low selection pressure or a high rate of mutation (which comes with small populations) can broaden the range of a species whereas intense selection pressure or a low mutation rate can severely limit a species to the very peak of local fitness. The third diagram shows what happens when the landscape itself shifts, and the population has to evolve to shift with it.

The bottom row explores how small populations respond to inbreeding by wandering ineffectively. The best mode of exploration Wright deemed the final diagram, showing how a species can divide into an array of races that interact with one another. That jostling crowd explores well, and it can respond to opportunity.

Fitness landscapes express so much so economically. There's no better way, for example, to show the different modes of evolution of a remote oceanic island and a continental jungle. The jungle is dense and "rugged" with steep peaks and valleys, isolating countless species on their tiny peaks of high specialization. The island, with its few species, is like a rolling landscape of gentle hills with species casually wandering over them, evolving into a whole array of Darwin's finches, say. The island creatures and plants "lazily" become defenseless against invaders from the mainland.

You realize that for each species, its landscape consists almost entirely of other species, all of them busy evolving right back. That's co-evolution. We are all each other's fitness landscapes.

Einstein's Photons

My favorite deep, elegant and beautiful explanation is Albert Einstein's 1905 proposal that light consists of energy quanta, today called photons. Actually, it is little known, even among physicists, but extremely interesting how Einstein came to this position. It is often said that Einstein invented the concept to explain the photoelectric effect. Certainly, that is part of Einstein's 1905 publication, but only towards its end. The idea itself is much deeper, more elegant and, yes, more beautiful.

Imagine a closed container whose walls are at some temperature. The walls are glowing, and as they emit radiation, they also absorb radiation. After some time, there will be some sort of equilibrium distribution of radiation inside the container. This was already well known before Einstein. Max Planck had introduced the idea of quantization that explained the energy distribution of the radiation inside such a volume. Einstein went a step further. He studied how orderly the radiation is distributed inside such a container. For physicists, entropy is a measure of disorder.

To consider a simple example, it is much more probable that books, notes, pencils, photos, pens etc. are cluttered all over my desk than that they are well ordered forming a beautiful stack. Or, if we consider a million atoms inside a container, it is much more probable that they are more or less equally distributed all over the volume of the container than that they are all collected in one corner. In both cases, the first state is less orderly: when the atoms fill a larger volume they have a higher entropy than the second one mentioned. The Austrian physicist Ludwig Boltzmann had shown that the entropy of a system is a measure of how probable its state is.

Einstein then realized in his 1905 paper that the entropy of radiation (including light) changes in the same mathematical way with the volume as for atoms. In both cases, the entropy increases with the logarithm of that volume. For Einstein this could not just be a coincidence. Since we can understand the entropy of the gas because it consists of atoms, the radiation consists also of particles that he calls energy quanta.

Einstein immediately applied his idea for example to his well-known application of the photoelectric effect. But he also realizes very soon a fundamental conflict of the idea of energy quanta with the well-studied and observed phenomenon of interference.

The problem is simply how to understand the two-slit interference pattern. This is the phenomenon that, according to Richard Feynman, contains "the only mystery" of quantum physics. The challenge is very simple. When we have both slits open, we obtain bright and dark stripes on an observation screen, the interference fringes. When we have only one slit open, we get no stripes, no fringes, but a broad distribution of particles. This can easily be understood on the basis of the wave picture. Through each of the two slits, a wave passes, and they extinguish each other at some places of the observation screen and at others, they enforce each other. That way, we obtain dark and bright fringes.

But what to expect if the intensity is so low that only one particle at a time passes through the apparatus? Following Einstein's realist position, it would be natural to assume that the particle has to pass through either slit. We can still do the experiment by putting a photographic plate at the observation screen and sending many photons in, one at a time. After a long enough time, we look at the photographic plate. According to Einstein, if the particle passes through either slit, no fringes should appear, because, simply speaking, how should the individual particle know whether the other slit, the one it does not pass through, is open or not. This was indeed Einstein's opinion, and he suggested that the fringes only appear if many particles go through at the same time, and somehow interact with each other such that they make up the interference pattern.

Today, we know that the pattern even arises if we have such low intensities that only one, say, photon per second passes through the whole apparatus. If we wait long enough and look at the distribution of all of them, we get the interference pattern. The modern explanation is that the interference pattern only arises if there is no information present anywhere in the Universe through which slit the particle passes. But even as Einstein was wrong here, his idea of the energy quanta of light, today called photons pointed far into the future.

In a letter to his friend Habicht in the same year of 1905, the miraculous year where he also wrote his Special Theory of Relativity, he called the paper proposing particles of light "revolutionary". As far as is known, this was the only work of his that he ever called revolutionary. And therefore it is quite fitting that the Nobel Prize was given to him for the discovery of particles of light. This was the Nobel Prize of 1921. That the situation was not as clear a few years before is witnessed by a famous letter signed by Planck, Nernst, Rubens and Warburg, suggesting Einstein for membership in the Prussian Academy of Sciences in 1913. They wrote: "the fact that he (Einstein) occasionally went too far should not be held too strongly against him. Not even in the exact natural sciences can there be progress without occasional speculation." Einstein's deep, elegant and beautiful explanation of the entropy of radiation, proposing particles of light in 1905, is a strong case in point for the usefulness of occasional speculation. 

The Inductive Economy of An Elegant Idea

An elegant and beautiful explanation is, to me, one that corrals a herd of seemingly unrelated facts within a single unifying concept. In our explorations of the worlds, including our own, that orbit the Sun, and in our attempts to find from these efforts what is special and what is commonplace about our own planet, I can think of two examples of this.

The first is an idea that was originally offered in the 1912 but met with such extreme hostility from the scientific establishment—not an unusual response, by the way, to an original idea—that it wasn't generally accepted until 50 years later. By that time, the sheer weight of evidence supporting it became so overwhelming that the notion was rendered irrefutable. And that notion was plate tectonics.

It could be said that the first indications of plate motions, though of course not recognized as such at the time, came from the observations of the early explorers, like Magellan, who noticed the puzzle-like fit of the continents, Africa and South America, for instance, on their maps. Fast forward to the early 20th century…Alfred Wegener, a German geophysicist, proposes movement of the continents (continental drift), to explain this hand-in-glove fit. Having no explanation, however, for how the continents could actually move, he was laughed out of the room.

But the evidence continued to mount: fossils, rock types, ancient climates were shown to be similar within widely separated geographical regions, like the east coast of South America and the west coast of Africa. Studies of magnetized rocks, which if stationary will always indicate a consistent direction to the north magnetic pole regardless where on the globe they form, indicated that either the north pole location varied throughout time or that the rocks themselves were not formed where they are found today. Finally, by the 1960s, it was clear that many of the Earth's presently active geological phenomena, such as the strongest earthquakes and volcanoes, were found within distinct, sinuous belts that wrapped around the planet and carved the Earth's surface into distinct bounded regions. Furthermore, studies of rocks on the floors of the Earth's oceans revealed an alternating north-up/north-down magnetic striping pattern that could only be explained by the upwelling of molten lava from below, creating new oceanic floor, and the consequent spreading of the old floor, pushing the continents farther apart with time. We now know that the tectonic forces driving the motions of the Earth's crustal plates arise from the convective upwelling and downwelling currents of molten rock in the Earth's mantle that drag around the solid plates sitting atop them.

In the end, the notion that bits of the Earth's surface can drift over time is a glorious example of a simple, efficient and even elegant idea that was eventually proven correct yet so radical for its time, it was scorned.

The second is more or less an extraterrestrial version of the same. In an historic mission not unlike Homer's Odyssey, two identical spacecraft—Voyager I and II—spent the 1980s touring the planetary systems of Jupiter, Saturn, Uranus and Neptune. And the images they returned provided humanity its first detailed views of these planets and the moons and rings surrounding them.

Jupiter was the gateway planet, the first of the four encountered, and it was there that we learned just how complex and presently active other planetary bodies could be. Along with the stunningly active moon, Io, which sported at the time about 9 large volcanic eruptions, Voyager imaged the surface of Jupiter's icy moon, Europa. Just a bit smaller than our own Moon, Europa's surface was clearly young, rather free of craters, and scored with a complex pattern of cracks and fractures that were cycloidal in shape and continuous, with many 'loops', like the scales on a fish. From these discoveries and others, it was inferred that Europa might have a thin crust overlying either warm, soft ice or perhaps even liquid water, though how the fracture pattern came to look the way it does was a mystery. The idea of a sub-surface ocean was enticing for the implicit possibility of a habitable zone for extraterrestrial life.

A follow-on spacecraft, Galileo, arrived at Jupiter in 1995 and before too long got an even better look at Europa's cracked ice shell and its cycloidal fractures. It became clear to researchers at the University of Arizona's Lunar and Planetary Lab that the cycloidal fractures, and even their detailed characteristics, like the shapes of the cycloidal segments, and the existence of, the distance between, and orientations of the cusps, could all be explained by the stresses across the moon's thin ice shell created by the tides raised on it by Jupiter. Europa's distance to Jupiter varies over the course of its orbit because of gravitational resonances with the other Jovian moons. And that varying separation causes the magnitude and direction of the tidal stresses on its surface to change. Under these conditions, if a crack in the thin ice shell is initiated at any location by these stresses, then that crack will propagate across the surface over the course of a Europan day and will take the shape of a cycloid. This will continue, day in and day out, scoring the surface of Europa in the manner that we find it today. Furthermore, tidal stresses would be inadequate to affect these kinds of changes to the moon's surface if its ice shell did not overlie a liquid ocean…an exciting possibility by anyone's measure.

And so, a whole array of features on the surface of one of Jupiter's most fascinating moons, the enormous complexity of the patterns they form, and the implication of a subterranean liquid water ocean in which extraterrestrial life might have taken hold, were explained and supported with one very simple, very easily demonstrated, and very elegant idea….an idea which itself, like that of plate tectonics, exemplifies the great beauty and economy derivable from logical induction, one of humankind's most demonstrably powerful intellectual devices.

The Principle of Least Action

Nature is lazy. Scientific paradigms and "ultimate" visions of the universe come and go, but the idea of "least action" has remained remarkably unperturbed. From Newton's classical mechanics to Einstein's general relativity to Schrödinger's quantum field theory, every major theory has been reformulated with this single principle, by Euler, Hilbert, and Feynman, respectively. The reliability of this framework suggests a form for whatever the next major paradigm shift may be.

Action is a strange quantity, in the units of energy multiplied by time. A principle of least action does not explicitly specify what will happen, like an equation of motion does, but simply asserts that the action will be the least of any conceivable actions. In some sense, the universe is maximally efficient. To be precise, the action integrated over any interval of time is always minimal. Euler and Lagrange discovered that not only is this principle true, but one can derive all of Newtonian physics from it. The Newtonian worldview was often characterized as "clockwork," both because clockwork was an apt contemporary technology, and because of the crucially absolute measurement of time.

In Einstein's relativity, absolute time was no longer possible, and totally new equations of motion had to be written. Now we have to deal with four-dimensional spacetime, rather than the familiar three-dimensional space and the special dimension of time. At speeds much less than the speed of light, a first-order approximation can transform Einstein's equations into Newton's, yet the resemblance is hardly obvious. However, the principle of least action remains much the same, but with a difference that intuitively connects to the essence of Einstein's insight: instead of just integrating over time, we must integrate over space too, with the speed of light serving as a constant exchange rate between spatial and temporal units. The essence of relativity is not its well-known consequences—time dilation, length dilation, or even E=mc^2. Rather, it is the more intuitive idea that space and time are simply different ways of looking at the same thing. Much more complicated mathematics is needed to derive Einstein's equations from this principle, but the legendary mathematician David Hilbert was able to do it. Maxwell's theory of electromagnetism, too, can be derived from the least action principle by a generalization of operators. Even more remarkably, combining the least-action tweaks that lead to Einstein's and Maxwell's equations respectively produces modern relativistic electromagnetism.

By this point you may be imagining that practically any physical theory can be formulated using the principle of least action. But in fact, many cannot —for instance, an early attempt at quantum electrodynamics, put forth by Paul Dirac. Such theories tend to have other issues that preclude their practical use; under many conditions, Dirac's theory prescribed infinite energies (clearly a dramatic difference from experiment). Quantum electrodynamics was later "fixed" by Feynman, a feat for which he won the Nobel Prize. In his Nobel lecture, he mentioned that the initial confirmation he was on the right track was that his version, unlike Dirac's, could be formulated as a principle of least action.

I believe it's reasonable to expect it will be possible to explain the next major physical theory using the least action framework, whatever it may be. Perhaps it will benefit us as scientists to explore our theories within this framework, rather than attempting to guess at once the explicit equations, and leaving the inevitable least action derivation as an exercise for some enterprising mathematician to work out.

The essential idea of least action transcends even the deepest of theoretical physics, and enters the domain of metaphysics. Claude Shannon derived a formula to quantify uncertainty, which von Neumann pointed out was identical to the formula used in thermodynamics to compute entropy. Edwin Jaynes put forth an interpretation of thermodynamics, in which entropy simply is uncertainty, nothing more and nothing less. Although the formal mathematical underpinnings remain controversial, I find it very worthwhile, at least as an intuitive explanation. Jaynes' followers propose a profound connection between action and information, such that the principle of least action and the laws of thermodynamics both derive from basic symmetries of logic itself. We need only accept that all conceivable universes are equally likely, a principle of least information. Under this assumption, we can imagine a smooth spectrum from metaphysics to physics, from the omniverse to the multiverse to the universe, where the fundamental axis is information, and the only fundamental law is that you can never assume more than you know.

Starting from nothingness, or the absence of information, there is a flowering of possible refinements toward specifying a universe, one of which leads to our Big Bang, to particles, fields and spacetime, and ultimately to intelligent life. The reason that we had a long period of stellar, planetary and biological evolution is that this is the path to intelligent life, which required the least action. Imagine how much action it would take to create intelligence directly from nothing! Universes without intelligent life might require even less action, but there is nobody in those universes to wonder where they came from.

At least for me, the least action perspective explains all known physics as well as the origin of our universe, and that sure is deep and beautiful.

"We Are Dreaming Machines That Construct Virtual Models Of The Real World"

The most beautiful and elegant explanation should be as strong and overwhelming as a brick smashing your head; it should break your life in two. For instance, as a result of that explanation, you should realize that even if you are dreaming your brain is active doing what he does best: creating models of reality or, in fact, creating the reality where you live in.

Descartes was aware of this fact and that's why he concluded "I think, therefore I am", cogito ergo sum. You can think of yourself as walking on a park, but this could be just a vivid dream. Therefore, it's not possible to conclude anything about your existence based on the apparent fact of walking. However, if you are really walking on a park, or dreaming, you are thinking, therefore existing. Dreaming is so similar to waking, that you can't trust any sensory information as proof of your existence. You can only trust the fact of thinking or, in contemporary words, the fact that your brain is active.

Dreaming and waking are similar cognitive states, as Rodolfo Llinás says in his masterpiece "I of the vortex". The only difference is that while dreaming, your brain is not perceiving or representing the external reality, it is emulating it and providing self-generated inputs.

The explanation is also shocking in its consequence. While waking we are also dreaming, concludes Llinás: "The waking state is a dreamlike state (…) guided and shaped by the senses, whereas regular dreaming does not involve the senses at all".

In both cases our brain generates models of reality.

With this explanation very few entities—the brain and the matter of reality—are enough to remind us how we create what is usually defined as "reality": "The only reality that exists for us is already a virtual one (…). We are basically dreaming machines that construct virtual models of the real world", says Llinás.

This is not only a beautiful explanation because of the poetic fact that reality is self-generated while dreaming, and partially generated while waking. Is there anything more beautiful than understanding how to create reality?

This is not only an elegant explanation because it shows our minuscule and entirely representative place in the ontological and physical reality, in the huge amount of matter defined as universe.

This explanation is overwhelming in practical terms because as a philosopher and social scientist, I cannot explain the physical or the social reality without considering that we live and move in a model of reality. Including the representational, creative and even ontological role of the brain, is a naturalization project usually omitted as a result of hyper-positivism and scientific fragmentation. From Descartes to Llinás, form the understanding of galaxies to the understanding of crime, this explanation should be relevant in most scientific enterprises.

Bounded Rationality As An Explanation For Many of Our Ills

Explanations that are extraordinary, both analytically and aesthetically, share among others, these properties: (a) they are often simpler compared to what was received wisdom, (b) they point to the more true cause as being some place quite removed from the phenomenon, and (c) they make you wish so much that you had come upon the explanation yourself.

Those of us who attempt to understand the mind, have a unique limitation to confront: the object that is the knower is also the known. The mind is the thing doing the explaining; the mind is also the thing to be explained. Distance from one's own mind, distance from attachments to the specialness of one's species or tribe, getting away from introspection and intuition (not as hypothesis generators but as answers and explanations) are all especially hard to achieve when what we seek to do is explain our own minds and those of others of our kind.

For this reason, my candidate for the most deeply satisfying explanation of recent decades is the idea of bounded rationality. The idea that human beings are smart by comparison to other species, but not smart enough by their own standards including behaving in line with basic axioms of rationality is a now a well-honed observation with deep empirical foundation in the form of discoveries in support.

Herbert Simon put one stake in the ground through the study of information processing and AI, showing that both people and organizations follow principles of behavior such as "satisficing" that constrain them to decent but not the best decisions. The second stake was placed by Kahneman and Tversky, who showed the stunning ways in even experts are error-prone—with consequences for not only their own health and happiness but that of their societies broadly.

Together the view of human nature that evolved over the past four decades has systematically changed the explanation for who we are and why we do what we do. We are error-prone in the unique ways in which we are, the explanation goes, not because we have malign intent, but because of the evolutionary basis of our mental architecture, the manner in which we remember and learn information, the way in which we are affected by those around us and so on. The reason we are boundedly rational is because the information space in which we must do our work is large compared to the capacities we have, including severe limits on conscious awareness, the ability to be able to control behavior, and to act in line even with our own intentions.

From these bounds on rationality generally, we can look also at the compromise of ethical standards—again the story is the same; that it is not intention to harm that's the problem. Rather the explanation lies in such sources are the manner in which some information plays a disproportionate role in decision making, the ability to generalize or overgeneralize, and the commonness of wrong doing that typify daily life. These are the more potent causes of the ethical failures of individuals and institutions.

The idea that bad outcomes result from limited minds that cannot store, compute and adapt to the demands of the environment is a radically different explanation of our capacities and thereby our nature. It's elegance and beauty comes from it placing the emphasis on the ordinary and the invisible rather than on specialness and malign motives. This seems not so dissimilar from another shift in explanation from god to natural section and it is likely to be equally resisted. 

What Time Is It? 

A few years ago, I heard said only old-fashioned folk wear watches. But I thought I would always wear a watch. Today I don't wear a watch.

How do I find the time? Either I do without or I keep my eyes fixed on a screen that has the time in the upper-right corner. It's gotten so that I resent that reality doesn't dispay the time in the upper-right corner. 

You Think, Therefore I Am

"I think, therefore I am." Cogito ergo sum. Remember this elegant and deep idea from René Descartes' Principles of Philosophy? The fact that a person is contemplating whether she exists, Descartes argued, is proof that she, indeed, actually does exist. With this single statement, Descartes knit together two central ideas of Western philosophy: 1) thinking is powerful, and 2) individuals play a big role in creating their own I's—that is, their psyches, minds, souls, or selves.

Most of us learn "the cogito" at some point during our formal education. Yet far fewer of us study an equally deep and elegant idea from social psychology: Other people's thinking likewise powerfully shapes the I's that we are. Indeed, in many situations, other people's thinking has a bigger impact on our own thoughts, feelings, and actions than do the thoughts we conjure while philosophizing alone.

In other words, much of the time, "You think, therefore I am." For better and for worse.

An everyday instance of how your thinking affects other people's being is the Pygmalion effect. Psychologists Robert Rosenthal and Lenore Jacobson captured this effect in a classic 1963 study. After giving an IQ test to elementary school students, the researchers told the teachers which students would be "academic spurters" because of their allegedly high IQs. In reality, these students' IQs were no higher than those of the "normal" students. At the end of the school year, the researchers found that the "spurters'" had attained better grades and higher IQs than the "normals." The reason? Teachers had expected more from the spurters, and thus given them more time, attention, and care. And the conclusion? Expect more from students, and get better results.

A less sanguine example of how much our thoughts affect other people's I's is stereotype threat. Stereotypes are clouds of attitudes, beliefs, and expectations that follow around a group of people. A stereotype in the air over African Americans is that they are bad at school. Women labor under the stereotype that they suck at math.

As social psychologist Claude Steele and others have demonstrated in hundreds of studies, when researchers conjure these stereotypes—even subtly, by, say, asking people to write down their race or gender before taking a test—students from the stereotyped groups score lower than the stereotype-free group. But when researchers do not mention other people's negative views, the stereotyped groups meet or even exceed their competition. The researchers show that students under stereotype threat are so anxious about confirming the stereotype that they choke on the test. With repeated failures, they seek their fortunes in other domains. In this tragic way, other people's thoughts deform the I's of promising students.

As the planet gets smaller and hotter, knowing that "You think, therefore I am" could help us more readily understand how we affect our neighbours and how our neighbours affect us. Not acknowledging how much we impact each other, in contrast, could lead us to repeat the same mistakes.

How The Availability Of Some Plants And Animals Can Explain Thousands Of Years Of Human History

One of the most elegant explanations I have encountered in the social sciences comes courtesy of Jared Diamond, and is outlined in his wonderful book "Guns, Germs, and Steel." Diamond attempts to answer an enormously complex and historically controversial question—why certain societies achieved such historical dominance over others—by appealing to a set of very basic differences in the physical environments from which these societies emerged (such as differences in the availability of plants and animals suitable for domestication).

These differences, Diamond argues, gave rise to a number of specific advantages (such as greater immunity to disease) that were directly responsible for the historical success of some societies.

I'm not an expert in this domain, and I accept that Diamond's explanation might be completely misguided. Yet the appeal to such basic mechanisms in order to explain such a wide set of complex observations is so deeply satisfying that I hope he is right.

Subjective Environment

Explanations tend to be at their most elegant, when science distills the meanderings of philosophy into fact. I was looking for explanations for an observation, when I came across the theory of "Umwelt" versus "Umfeld" (vaguely environment versus surroundings) by the Estonian biologist and forefather of biosemiotics Jakob von Uexküll. According to his definition "Umwelt" is the subjective environment as perceived and impacted by an organism, while "Umfeld" is the objective environment which encompasses and impacts all organisms in it's realm.

My observation had been a mere notion of the major difference between my native Europe and America, my adopted continent for a couple of decades. In Europe the present is perceived as the end point of history. In America the present is perceived as the beginning of the future. Philosophy or history, I hoped, would have an explanation for such a fundamental yet simple difference. Both can deliver parts of an explanation of course. The different paths the histories of ideas and the histories of the countries have taken just in the past 200 years are astounding.

Uexküll's definition of the subjective environment as published in his book Umwelt und Innnenwelt der Tiere (Environments and inner worlds of animals, published 1909 in the language of his German exile) puts both philosophy and history into perspective and context though. Distrusting theories he always wanted ideas to persist in nature. Putting his idea of the subjective environment to the test in the Indian Ocean, the Atlantic and the Mediterranean. He observed simple creatures like sea anemones, sea urchins and crustaceans. His most famous example to explain his theory was the tick though. Here he found a creature whose perception and actions could be defined by three parameters each. Ticks perceive their surroundings by the directions of up and down, by warm and cold and the presence or absence of butyric acid. Their actions to survive and procreate are crawling, waiting and gripping.

This model lead him not only to define environment as a subjective notion. He found the perception of time for any organism as subjective as the perception of space, defined by the very perceptions and actions that create the organism's subjective environment. If subjective time is defined by the experiences and actions of an organism, the context of a continent's history with its myriads of parameters turns philosophy and history into mere factors in a complex environment of collective perception. Now there was an elegant explanation for a rather simple observation. Making it even more elegant is the notion that in the context of a continent's evolution geography, climate, food and culture will weigh in as factors of the perception of the subjective environment and time as well, making it impossible to prove or disprove the explanation scientifically. Having rendered philosophy to just one of many parameters it thus reduces its efforts to discredit Jakob von Uexküll's definition of the subjective environment to mere meanderings. 

Falling Into Place: Entropy, Galileo's Frames of Reference, and the Desperate Ingenuity Of Life

The hardest choice I had to make in my early scientific life was whether to give up the beautiful puzzles of quantum mechanics, nonlocality, and cosmology for something equally arresting: To work instead on reverse engineering the code that natural selection had built into the programs that made up our species' circuit architecture. In 1970, the surrounding cultural frenzy and geopolitics made first steps toward a nonideological and computational understanding of our evolved design, "human nature", seem urgent; the recent rise of computer science and cybernetics made it seem possible; the almost complete avoidance of and hostility to evolutionary biology by behavioral and social scientists had nearly neutered those fields, and so made it seem necessary.

What finally pulled me over was that the theory of natural selection was itself such an extraordinarily beautiful and elegant inference engine. Wearing its theoretical lenses was a permanent revelation, populating the mind with chains of deductions that raced like crystal lattices through supersaturated solutions. Even better, it starts from first principles (such as set theory and physics), so much of it is nonoptional.

But still, from the vantage point of physics, beneath natural selection there remained a deep problem in search of an explanation: The world given to us by physics is unrelievedly bleak. It blasts us when it is not burning us or invisibly grinding our cells and macromolecules until we are dead. It wipes out planets, habitats, labors, those we love, ourselves. Gamma ray bursts wipe out entire galactic regions; supernovae, asteroid impacts, supervolcanos, and ice ages devastate ecosystems and end species. Epidemics, strokes, blunt force trauma, oxidative damage, protein cross-linking, thermal noise-scrambled DNA—all are random movements away from the narrowly organized set of states that we value, into increasing disorder or greater entropy. The second law of thermodynamics is the recognition that physical systems tend to move toward more probable states, and in so doing, they tend to move away from less probable states (organization) on their blind toboggan ride toward maximum disorder.

Entropy, then, poses the problem: How are living things at all compatible with a physical world governed by entropy, and, given entropy, how can natural selection lead over the long run to the increasing accumulation of functional organization in living things? Living things stand out as an extraordinary departure from the physically normal (e.g., the earth's metal core, lunar craters, or the solar wind). What sets all organisms—from blackthorn and alder to egrets and otters—apart from everything else in the universe is that woven though their designs are staggeringly unlikely arrays of highly tuned interrelationships—a high order that is highly functional. Yet as highly ordered physical systems, organisms should tend to slide rapidly back toward a state of maximum disorder or maximum probability. As the physicist Erwin Schrödinger put it, "It is by avoiding the rapid decay into the inert state that an organism appears so enigmatic."

The quick answer normally palmed off on creationists is true as far as it goes, but it is far from complete: The earth is not a closed system; organisms are not closed systems, so entropy still increases globally (consistent with the second law of thermodynamics) while (sometimes) decreasing locally in organisms. This permits but does not explain the high levels of organization found in life. Natural selection, however, can (correctly) be invoked to explain order in organisms, including the entropy-delaying adaptations that keep us from oxidizing immediately into a puff of ash.

Natural selection is the only known counterweight to the tendency of physical systems to lose rather than grow functional organization—the only natural physical process that pushes populations of organisms uphill (sometimes) into higher degrees of functional order. But how could this work, exactly?

It is here that, along with entropy and natural selection, the third of our trio of truly elegant scientific ideas can be adapted to the problem: Galileo's brilliant concept of frames of reference, which he used to clarify the physics of motion.

The concept of entropy was originally developed for the study of heat and energy, and if the only kind of real entropy (order/disorder) was the thermodynamic entropy of energy dispersal then we (life) wouldn't be possible. But with Galileo's contribution one can consider multiple kinds of order (improbable physical arrangements), each being defined with respect to a distinct frame of reference.

There can be as many kinds of entropy (order/disorder) as there are meaningful frames of reference. Organisms are defined as self-replicating physical systems. This creates a frame of reference that defines its kind of order in terms of causal interrelationships that promote the replication of the system (replicative rather than thermodynamic order). Indeed, organisms must be physically designed to capture undispersed energy, and like hydroelectric dams using waterfalls to drive turbines, they use this thermodynamic entropic flow to fuel their replication, spreading multiple copies of themselves across the landscape.

Entropy sometimes introduces copying errors into replication, but injected disorder in replicative systems is self-correcting. By definition the less well-organized are worse at replicating themselves, and so are removed from the population. In contrast, copying errors that increase functional order (replicative ability) become more common. This inevitable ratchet effect in replicators is natural selection.

Organisms exploit the trick of deploying different entropic frames of reference in many diverse and subtle ways, but the underlying point is that what is naturally increasing disorder (moving toward maximally probable states) for one frame of reference inside one physical domain can be harnessed to decrease disorder with respect to another frame of reference. Natural selection picks out and links different entropic domains (e.g., cells, organs, membranes) that each impose their own proprietary entropic frames of reference locally.

When the right ones are associated with each other, they do replicative work through harnessing various types of increasing entropy to decrease other kinds of entropy in ways that are useful for the organism. For example: oxygen diffusion from the lungs to the blood stream to the cells is the entropy of chemical mixing—falling toward more probable high entropy states, but increasing order from the perspective of replication-promotion.

Entropy makes things fall, but life ingeniously rigs the game so that when they do they often fall into place. 

Everything Is The Way It Is Because It Got That Way

This aphorism is attributed to the biologist and classicist D'Arcy Thompson, and it's an elegant summary of how Thompson sought to explain the shapes of things, from jellyfish to sand dunes to elephant tusks. I saw this quoted first in an Edge discussion by Daniel Dennett, who made the point that this insight applies to explanation more generally—all sciences are, to at least some extent, historical sciences. 

I think it's a perfect motto for my own field of developmental psychology. Every adult mind has two histories. There is evolution. Few would doubt that some of the most elegant and persuasive explanations in psychology appeal to the constructive process of natural selection. And there is development—how our minds unfold over time, the processes of maturation and learning. 

While evolutionary explanations work best for explaining what humans share, development can sometimes capture how we differ. This can be obvious: Nobody is surprised to hear that adults who are fluent in Korean have usually been exposed to Korean when they were children or that adults who practice Judaism have usually been raised as Jews. But other developmental explanations are rather interesting.

There is evidence that an adult's inability to see in stereo is due to poor vision during a critical period in childhood. Some have argued that the self-confidence of adult males is influenced by how young they were when they reached puberty (because of the boost in status caused by being bigger, even if temporarily, than their peers). It's been claimed that smarter adults are more likely to be firstborns (because later children find themselves in environments that are, on average, less intellectually sophisticated). Creative adults are more likely to be later-borns (because they were forced to find their own distinctive niches.) Romantic attachments in adults are influenced by their relationships as children with their parents. A man's pain-sensitivity later in life is influenced by whether or not he was circumcised as a baby.

With the exception of the stereo-vision example, I don't know if any of these explanations are true. But they are elegant and non-obvious, and some of them verge on beautiful. 

Germs Cause Disease

The germ theory of disease has been very successful, particularly if you care about practical payoffs, like staying alive. It explains how disease can rapidly spread to large numbers of people (exponential growth), why there are so many different diseases (distinct pathogen species), and why some kind of contact (sometimes indirect) is required for disease transmission.

In modern language, most disease syndromes turn out to be caused by tiny self-replicating machines whose genetic interests are not closely aligned with ours.

In fact, germ theory has been so successful that it almost seems uninteresting. Once we understood the causes of cholera and pneumonia and syphilis, we got rid of them, at least in the wealthier countries. Now we're at the point where people resist the means of victory—vaccination for example—because they no longer remember the threat.

It is still worth studying—not just to fight the next plague, but also because it has been a major factor in human history and human evolution. You can't really understand Cortez without smallpox or Keats without tuberculosis. The past is another country—don't drink the water.

It may well explain patterns that we aren't even supposed to see, let alone understand. For example, human intelligence was, until very recently, ineffective at addressing problems causing by microparasites, as William McNeill pointed out in Plagues and Peoples. Those invisible enemies played a major role in determining human biological fitness—more so in some places than others. Consider the implications.

Lastly, when you leaf through a massively illustrated book on tropical diseases and gaze upon an advanced case of elephantiasis, or someone with crusted scabies, you realize that any theory that explains that much ugliness just has to be true. 

Lemons are Fast

When asked to put lemons on a scale between fast and slow almost everyone says 'fast', and we have no idea why. Maybe human brains are just built to respond that way. Probably. But how does that help? It's an explanation of sorts but it seems to be a stopping point when we wanted to know more. This leads us to ask what we want from an explanation: one that's right, or one that satisfies us? Things that were once self-evident are now known to be false. A straight line is obviously the shortest distance between two points until we think that space is curved. What satisfies our way of thinking need not reflect reality. Why expect a simple theory of a complex world?

Wittgenstein had interesting things to say about what we want from explanations and he knew different things could serve. Sometimes we just need more information; sometimes, we need to examine a mechanism, like a valve, or a pulley, to understand how it works; while sometimes what we need is a way of seeing something familiar in a new light, to see it as it really is. He also knew there were times when explanations won't do. 'To the man who has lost in love', he asks, 'what will help him? An explanation?' The question clearly invites the answer, no.

So what of the near universal response to the seemingly meaningless question of whether lemons are fast or slow? To be told that our brains are simply built to respond that way doesn't satisfy us. But it's precisely when an explanation leaves us short that it spurs us to greater effort.

It's the start of the story, not the end. For the obvious next question to ask is why are human brains built this way? What purpose could it serve? And here the phenomenon of automatic associations may give us a deep clue about the way the mind works because it's symptomatic of what we call cross-modal correspondences: non-arbitrary associations between features in one sense modality with features in another.

There are cross-modal correspondences between taste and shape, between sound and vision, between hearing and smell, many of which are being investigated by neuroscientist Charles Spence and philosopher Ophelia Deroy. These unexpected connections are reliable and shared, unlike cases of synaesthesia, which are idiosyncratic—though individually consistent. And the reason we make these connections in the brain is to give us multiple fixes on objects in the environment that we can both hear and see. It also allows us to communicate elusive aspects of our experience.

We often say that tastes are hard to describe, but when we realise that we can change vocabulary and talk about a taste as round or sharp new possibilities open up. Musical notes are high or low; sour tastes are high, and bitter notes low. Smells can have low notes and high notes. You can feel low, or be incredibly high. This switching of vocabularies allows us to utilise well-understood sensory modalities to map various possibilities of experience.

Advertisers know this intuitively and exploit cross-modal correspondences between abstract shapes and particular products, or between sounds and sights. Angular shapes conjure up carbonated water not still, while an ice cream called 'Frisch' would be thought creamier than one called 'Frosch'. Notice, too, how many successful companies have names starting with the /k/ sound, and how few with /s/. These associations set up expectations in the mind that not only help us perceive but may shape our experiences.

And it is not just vocabularies that we use. In his nineteenth century tract on the Psychology of Architecture, Heinrich Wofflin tells us that it's because we have bodies, and are subject to gravity, bending and balance, that we can appreciate the shape of buildings, and columns, by feeling an empathy for their weight and strain. Physical forms possess a character only because we possess a body.

This idea has led to recent insights into aesthetic appreciation in the work of Chris McManus at UCL. Like all good explanations it spawns more explanations and further insights. It's another example of how we use the interaction of sensory information to shape our perceptions and help us to understand and respond to the world around us. Like all good explanations it spawns more explanations and further insights. So the fact that we all think that lemons are fast may be a big part of the reason why we are so smart. 

Russell's Theory of Descriptions

My favourite example of an elegant and inspirational theory in philosophy is Russell's Theory of Descriptions. It did not prove definitive, but it prompted richly insightful trains of enquiry into the structure of language and thought.

In essence Russell's theory turns on the idea that there is logical structure beneath the surface forms of language, which analysis brings to light; and when this structure is revealed we see what we are actually saying, what beliefs we are committing ourselves to, and what conditions have to be satisfied for the truth or falsity of what is thus said and believed.

One example Russell used to illustrate the idea is the assertion 'the present King of France is bald,' said when there is no King of France. Is this assertion true or false? One response might be to say that it is neither, since there is no King of France at present. But Russell wished to find an explanation for the falsity of the assertion which did not dispense with bivalence in logic, that is, the exclusive alternative of truth and falsity as the only two truth-values.

He postulated that the underlying form of the assertion consists in the conjunction of three logically more basic assertions: (a) there is something that has the property of being King of France, (b) there is only one such thing (this takes care of the implication of the definite article 'the') (c) and that thing has the further property of being bald. In the symbolism of first-order predicate calculus, which Russell took to be the properly unambiguous rendering of the assertion's logical form (I omit strictly correct bracketing so as not to clutter):

(Ex)Kx & [(y)Ky— >y=x] & Bx

which is pronounced 'there is an x such that x is K; and for anything y, if y is K then y and x are identical (this deals logically with 'the' which implies uniqueness); and x is B,' where K stands for 'has the property of being King of France' and B stands for 'has the property of being bald.' 'E' is the existential quantifier 'there is...' or 'there is at least one...' and '(y)' stands for the universal quantifier 'for all' or 'any.'

One can now see that there are two ways in which the assertion can be false; one is if there is no x such that x is K, and the other is if there is an x but x is not bald. By preserving bivalence and stripping the assertion to its logical bones Russell has provided what Frank Ramsey wonderfully called 'a paradigm of philosophy.' 

To the irredeemable sceptic about philosophy all this doubtless looks like 'drowning in two inches of water' as the Lebanese say; but in fact it is in itself an exemplary instance of philosophical analysis, and it has been very fruitful as the ancestor of work in a wide range of fields, ranging from the contributions of Wittgenstein and W. V. Quine to research in philosophy of language, linguistics, psychology, cognitive science, computing and artificial intelligence.

We're Apes

Phylogenetically, and in terms of their ecological niche and morphology, apes are less similar to small monkeys than to paleolithic humans. Therefore, absent evidence to the contrary, we should expect that we can predict ape behavior better by looking at paleolithic human behavior than by looking at monkey behavior. This is a testable claim. Naive subjects can try to predict ape behavior by using different pools of evidence, information about either monkeys or paleolithic humans. The amount that one can know about a by observing b is correlated to the amount one can know about b by observing a. This consideration really should narrow the range of hypotheses we consider when speculating upon our innate behavior. If all other apes and monkeys possess a feature, including 'innate behavior' in so far as 'innate behavior' is a valid conceptual construct, we probably also possess that feature.

It may not be much, as a theory of psychology, but it's a start.

While making some correct predictions, this model certainly has its failures. Some of these failures seem relatively unthreatening. For instance, because we eat far less fruit than most monkeys or apes do, we tend to have much lower concentrations of vitamin C in our blood than do other primates. We can explain this difference easily because we can conceive of a clear difference between the concepts 'innate biochemistry' and 'biochemistry'. Other theoretical failures are more perplexing. One might speculate that paleolithic humans lack thick body hair because they use fire. Some day, differences between preserved Habilus and Erectus tissues might even partially confirm this, but one then has to ask why they and Sapiens but no other apes can use fire. Habitat is surely somewhat relevant, as most apes live in very heavily wooded locations, which present difficulties in the use of fire. Other apes also possess generally inferior tool-using abilities when compared to Habilus, Erectus or Sapiens. Most distressing, paleolithic humans tend to produce a much larger range of vocalizations than do other primates, a behavior that seems more typically birdlike. 

Epigenetics

To me, epigenetics is the most monumental explanation to emerge in the social and biological sciences since Darwin proposed his theories of Natural Selection and Sexual Selection. Over 2,500 articles, many scientific meetings, the formation of the San Diego Epigenome Center as well as other institutes, a five-year Epigenomics Program launched in 2008 by the National Institutes of Health, and many other institutions, academic forums and people are now devoted to this new field. Although epigenetics has been defined in several ways, all are based in the central concept that environmental forces can affect gene behavior, either turning genes on or off. As an anthropologist untrained in advanced genetics, I won't attempt to explain the processes involved, although two basic mechanisms are known: one involves molecules known as methyl-groups that latch on to DNA to suppress and silence gene expression; the other involves molecules known as acetyl-groups which activate and enhance gene expression.

The consequences of epigenetic mechanisms are likely to be phenomenal. Scientists now hypothesize that epigenetic factors play a role in the etiology of many diseases, conditions and human variations—from cancers, to clinical depression and mental illnesses, to human behavioral and cultural variations.

Take the Moroccan Amazighs or Berbers, people with highly similar genetic profiles who now reside in three different environments: some roam the deserts as nomads; some farm the mountain slopes; some live in the towns and cities along the Moroccan coast. And depending on where they live, up to one-third of their genes are differentially expressed, reports researcher Youssef Idaghdour.

 For example, among the urbanites, some genes in the respiratory system are switched on—perhaps, Idaghdour suggests, to counteract their new vulnerability to asthma and bronchitis in these smoggy surroundings. Idaghdour and his colleague Greg Gibson, propose that epigenetic mechanisms have altered the expression of many genes in these three Berber populations, producing their population differences.

 Psychiatrists, psychologists and therapists have long been preoccupied with our childhood experiences, specifically how these sculpt our adult attitudes and behaviors. Yet they have focused on how the brain integrates and remembers these occurrences. Epigenetic studies provide a different explanation.

As an example, mother rats that spend more time licking and grooming their young during the first week after birth produce infants who later become better adjusted adults. And researcher Moshe Szyf proposes that this behavioral adjustment occurs because epigenetic mechanisms are triggered during this "critical period," producing a more active version of a gene that encodes a specific protein. Then this protein, via complex pathways, sets up a feedback loop in the hippocampus of the brain—enabling these rats to cope more efficiently with stress.

These behavioral modifications remain stable through adulthood. However, Szyf notes that when specific chemicals were injected into the adult rat's brain to alter these epigenetic processes and suppress this gene expression, well-adjusted rats became anxious and frightened. And when different chemicals are injected to trigger epigenetic processes that enhance the expression of this gene instead, fearful adult rats (that had received little maternal care in infancy) became more relaxed.

 Genes hold the instructions; epigenetic factors direct how those instructions are carried out. And as we age, scientists report, these epigenetic processes continue to modify and build who we are. Fifty-year-old twins, for example, show three times more epigenetic modifications than do three-year-old twins; and twins reared apart show more epigenetic alterations than those who grow up together. Epigenetic investigations are proving that genes are not destiny; but neither is the environment—even in people.

Shelley Taylor has shown this. Studying an allele (genetic variant) in the serotonin system, she and colleagues were able to demonstrate that the symptoms of depression are visible only when this allele is expressed in combination with specific environmental conditions. Moreover, Taylor maintains that individuals growing up in unstable households are likely to suffer all their lives with depression, anxiety, specific cancers, heart disease, diabetes or obesity. Epigenetics at work? Probably.

 Even more remarkable, some epigenetic instructions are passed from one generation to the next. Trans-generational epigenetic modifications are now documented in plants and fungi, and have been suggested in mice. Genes are like the keys on a piano; epigenetic processes direct how these keys are played—modifying the tune, even passing these modifications to future generations. Indeed, in 2010, scientists wrote in Science magazine that epigenetic systems are now regarded as "heritable, self-perpetuating and reversible."

 If epigenetic mechanisms can not only modulate our intellectual and physical capacities, but also pass these alterations to our descendants, epigenetics has immense and profound implications for the origin, evolution and future of life on earth. In coming decades scientists studying epigenetics may come to understand how myriad environmental forces impact our health and longevity in specific ways, find cures for many human diseases and conditions, and explain intricate variations in human personality.

The 18^th century philosopher, John Locke, was convinced that the human mind is an empty slate upon which the environment inscribes personality. With equal self-assurance, others have been convinced that genes orchestrate our development, illnesses and life styles. Yet social scientists had failed for decades to explain the mechanisms governing behavioral variations between twins, family members and culture groups. And biological scientists had failed to pinpoint the genetic foundations of many mental illnesses and complex diseases. The central mechanism to explain these complex issues has been found.

 I am hardly the first to hail this new field of biology as revolutionary—the fundamental process by which nature and nurture interact. But to me as an anthropologist long trying to take a middle road in a scientific discipline intractably immersed in nature-versus-nurture warfare, epigenetics is the missing link.

Back To The Beginning, The Mere Word

Richard Rorty's transformation of "survival of the fittest" to "whatever survives survives" is not in itself my favorite explanation, though I find it immensely satisfying, but it enacts a wholesome return to language away from the most rococo fantasies of science. In this case, a statement that looks to describe history and biology—controversially, no less—drops into a foundational locution, a tautology. Back to the beginning, the mere Word. Anytime an explanation, for anything, returns us to language, and its dynamics, I'm satisfied. Exhilarated.

Frames of Reference

Deep and elegant explanations relate to natural or social phenomena and the observer often has no place in them. As a young student I was fascinated to understand how frames of reference work, i.e., to learn what it means to be an observer.

The reference frame concept is central in physics and astronomy. For example, the study of flows relies most often on two basic frames: one in which the flow is described as it moves through space, called an Eulerian frame, and another—called a Lagrangian frame, which moves with the flow, stretching and bending as it goes. The equations of motion in the Eulerian frame seemed intuitively obvious to me, but I felt exhilarated when I understood the same flow described by equations in the Lagrangian frame.

It is beautiful: let's think of a flow of water—a winding river. You are perched on a hill by the riverbank observing the water flow marked by a multitude of floating tree leaves. The banks of the river, the details of the surroundings—they provide a natural coordinate system, just as you would on a geographical map—you could almost create a mental image of fixed criss crossing lines—your frame of reference. The river flow of water moves through that fixed map: you are able to describe the twists and turns of the currents and their changing speed, all thanks to this fixed Eulerian frame of reference, named after Leonhard Euler (1707-1783).

It turns out that you could describe the flow with equal success if, instead of standing safely on the top of the hill, you plunged into the river and floated downstream, observing the whirling motions of the tree leaves all around you. Your frame of reference—the one named after Joseph-Louis Lagrange (1736-1813), is no longer fixed; instead you are describing all motions as relative to you and to each other. Your description of the flow will match exactly the description you achieved by observing from the hill, although the mathematical equations appear unrecognizably different.

To younger me, back then, the transformation between the two frames looked like magic. It was not deep perhaps, but it was elegant, and extremely helpful. However, it was also just the easy start of a journey—a journey that would pull the old frames of reference out from under me. It started with the naïve unmoving Earth as the absolute frame of Aristotle, soon to be rejected and replaced by Galileo with a frame of reference in which motion is not absolute—oh, how I loved floating with Lagrange down Euler's river!, only to be unsettled again by the special relativity of Einstein and trying to comprehend the loss of simultaneity. And a loss it was.

A fundamental shift in our frame of reference, especially the one that defines our place in the world, affects deeply each and every one of us personally. We live and learn, the next generation is born into the new with no attachment to the old. In science it is easy. Human frames of reference go beyond mathematics, physics, and astronomy. Do we know how to transform between human frames of reference successfully? Are they more often than not "Lagrangian" and relative? Perhaps we could take a cue from science and find an elegant solution. Or at least—an elegant explanation.

Einstein's Revenge: The New Geometric Quantum

The modern theory of the quantum has only recently come to be understood to be even more exquisitely geometric than Einstein's General Relativity. How this realization unfolded over the last 40 years is a fascinating story that has, to the best of my knowledge, never been fully told as it is not particularly popular with some of the very people responsible for this stunning achievement.

To set the stage, recall that fundamental physics can be divided into two sectors with separate but maddeningly incompatible advantages. The gravitational force has, since Einstein's theory of general relativity, been admired for its four dimensional geometric elegance. The quantum, on the other hand encompasses the remaining phenomena, and is lauded instead for its unparalleled precision, and infinite dimensional analytic depth.

The story of the geometric quantum begins at some point around 1973-1974, when our consensus picture of fundamental particle theory stopped advancing. This stasis, known as the 'Standard Model', seemed initially like little more than a temporary resting spot on the relentless path towards progress in fundamental physics, and theorists of the era wasted little time proposing new theories in the expectation that they would be quickly confirmed by experimentalists looking for novel phenomena. But that expected entry into the promised land of new physics turned into a 40-year period of half-mad tribal wandering in an arid desert, all but devoid of new phenomena.

Yet just as particle theory was failing to advance in the mid 1970s, something amazing was quietly happening over lunch at the State University of New York at Stony Brook. There, Nobel physics laureate CN Yang and geometer (and soon to billionaire) Jim Simons had started an informal seminar to understand what, if anything, modern geometry had to do with quantum field theory. The shocking discovery that emerged from these talks was that both geometers and quantum theorists had independently gotten hold of different collections of insights into a common structure that each group had independently discovered for themselves. A Rosetta stone of sorts called the Wu-Yang dictionary was quickly assembled by the physicists, and Isadore Singer of MIT took these results from Stony Brook to his collaborator Michael Atiyah in Oxford where their research with Nigel Hitchin began a geometric renaissance in physics inspired geometry that continues to this day.

While the Stony Brook history may be less discussed by some of today's younger mathematicians and physicists, it is not a point of contention between the various members of the community. The more controversial part of this story, however, is that a hoped for golden era of theoretical physics did not emerge in the aftermath to produce a new consensus theory of elementary particles. Instead the interaction highlighted the strange idea that, just possibly, Quantum theory was actually a natural and elegant self-assembling body of pure geometry that had fallen into an abysmal state of pedagogy putting it beyond mathematical recognition. By this reasoning, the mathematical basket case of quantum field theory was able to cling to life and survive numerous near death experiences in its confrontations with mathematical rigor only because it was being underpinned by a natural infinite dimensional geometry, which is to this day still only partially understood.

In short, most physicists were trying and failing to quantize Einstein's geometric theory of gravity because they were first meant to go in the opposite and less glamorous direction of geometrizing the quantum instead. Unfortunately for Physics, mathematicians had somewhat dropped the ball by not sufficiently developing the geometry of infinite dimensional systems (such as the Standard Model), which would have been analogous to the 4-dimensional Riemannian geometry appropriated from mathematics by Einstein.

This reversal could well be thought of as Einstein's revenge upon the excesses of quantum triumphalism, served ice cold decades after his death: the more researchers dreamed of becoming the Nobel winning physicists to quantize gravity, the more they were rewarded only as mathematicians for what some saw as the relatively remedial task of geometrizing the quantum. The more they claimed that the 'power and glory' of string theory (a failed piece of 1970s sub-atomic physics which has mysteriously lingered into the 21^st century) was the 'only game in town', the more it suggested that it was the string theory-based unification claims that, in the absence of testable predictions, were themselves sinking with a glug to the bottom of the sea.

What we learned from this episode was profound. Increasingly, the structure of Quantum Field Theory appears to be a purely mathematical input-output machine where our physical world is but one of many natural inputs that the machine is able to unpack from initial data. In much the way that a simple one-celled human embryo self-assembles into a trillion celled infant of inconceivable elegance, the humble act of putting a function (called an 'action' by physicists) on a space of geometric waves appears to trigger a self-assembling mathematical Rube-Goldberg process which recovers the seemingly intricate features of the formidable quantum as it inexorably unfolds. It also appears that the more geometric the input given to the machine, the more the unpacking process conspires to steer clear of the pathologies which famously afflict less grounded quantum theories. It is even conceivable that sufficiently natural geometric input could ultimately reveal the recent emphasis on 'quantizing gravity' as an extravagant mathematical misadventure distracting from Einstein's dream of a unified physical field. Like genius itself, with the right natural physical input, the new geometric quantum now appears to many mathematicians and physicists to be the proverbial fire that lights itself.

Yet, if the physicists of this era failed to advance the standard model, it was only in their own terms that they went down to defeat. Just as in an earlier era in which physicists retooled to become the first generation of molecular biologists, their viewpoints came to dominate much of modern geometry in the last four decades, scoring numerous mathematical successes that will stand the tests of time. Likewise their quest to quantize gravity may well have backfired, but only in the most romantic and elegant way possible by instead geometrizing the venerable quantum as a positive externality.

But the most important lesson is that, at a minimum, Einstein's minor dream of a world of pure geometry has largely been realized as the result of a large group effort. All known physical phenomena can now be recognized as fashioned from the pure, if still heterogeneous, marble of geometry through the efforts of a new pantheon of giants. Their achievements, while still incomplete, explain in advance of unification that the source code of the universe is overwhelmingly likely to determine a purely geometric operating system written in a uniform programming language. While that leaves Einstein's greater quest for the unifying physics unfinished, and the marble something of a disappointing patchwork of motley colors, it suggests that the leaders during the years of the Standard Model stasis have put this period to good use for the benefit of those who hope to follow. 

Our Universe Grew Like A Baby

What caused our Big Bang? My favorite deep explanation is that our baby universe grew like a baby human—literally. Right after your conception, each of your cells doubled roughly daily, causing your total number of cells to increase day by day as 1, 2, 4, 8, 16, etc. Repeated doubling is a powerful process, so your Mom would have been in trouble if you'd kept doubling your weight every day until you were born: after nine months (about 274 doublings), you would have weighed more than all the matter in our observable universe combined. 

Crazy as it sounds, this is exactly what our baby universe did according to the inflation theory pioneered by Alan Guth and others: starting out with a speck much smaller and lighter than an atom, it repeatedly doubled its size until it was more massive than our entire observable universe, expanding at dizzying speed. And it doubled not daily but almost instantly. In other words, inflation created our mighty Big Bang out of almost nothing, in a tiny fraction of a second. By the time you reached about 10 centimeters in size, your expansion had transitioned from accelerating to decelerating. In the simplest inflation models, our baby universe did the same when it was about 10 centimeters in size, its exponential growth spurt slowing to a more leisurely expansion where hot plasma diluted and cooled and its constituent particles gradually coalesced into nuclei, atoms, molecules, stars and galaxies.

Inflation is like a great magic show—my gut reaction is: "This can't possibly obey the laws of physics!'' 

Yet under close enough scrutiny, it does. For example, how can one gram of inflating matter turn into two grams when it expands? Surely, mass can't just be created from nothing? Interestingly, Einstein offered us a loophole through his special relativity theory, which says that energy E and mass m are related according to the famous formula E=mc², where c is the speed of light.

This means that you can increase the mass of something by adding energy to it. For example, you can make a rubber band slightly heavier by stretching it: you need to apply energy to stretch it, and this energy goes into the rubber band and increases its mass. A rubber band has negative pressure because you need to do work to expand it. Similarly, the inflating substance has to have negative pressure in order to obey the laws of physics, and this negative pressure has to be so huge that the energy required to expand it to twice its volume is exactly enough to double its mass. Remarkably, Einstein's theory of General Relativity says that this negative pressure causes a negative gravitational force. This in turn causes the repeated doubling, ultimately creating everything we can observe from almost nothing.

To me, the hallmark of a deep explanation is that it answers more than you ask. And inflation has proven to be the gift that keeps on giving, churning out answer after answer. It explained why space is so flat, which we've measured to about 1% accuracy. It explained why on average, our distant universe looks the same in all directions, with only 0.002% fluctuations from place to place. It explained the origins of these 0.002% fluctuations as quantum fluctuations stretched by inflation from microscopic to macroscopic scales, then amplified by gravity into today's galaxies and cosmic large scale structure. It even explained the cosmic acceleration that nabbed the 2011 physics Nobel Prize as inflation restarting, in slow motion, doubling the size of our universe not every split second but every 8 billion years, transforming the debate from whether inflation happened or not to whether it happened once or twice. 

It's now becoming clear that inflation is an explanation that doesn't stop—inflating or explaining. 

Just as cell division didn't make merely one baby and stop, but a huge and diverse population of humans, it looks like inflation didn't make merely one universe and stop, but a huge and diverse population of parallel universes, perhaps realizing all possible options for what we used to think of as physical constants. Which would explain yet another mystery: the fact that many constants in our own universe are so fine-tuned for life that if they changed by small amounts, life as we know it would be impossible—there would be no galaxies or no atoms, say. Even though most of the parallel universes created by inflation are stillborn, there will be some where conditions are just right for life, and it's not surprising that this is where we find ourselves.

Inflation has given us an embarrassment of riches—and embarrassing it is... Because this infinity of universes has brought about the so-called measure problem, which I view as the greatest crisis facing modern physics. Physics is all about predicting the future from the past, but inflation seems to sabotage this. Our physical world is clearly teeming with patterns and regularities, yet when we try quantifying them to predict the probability that something particular will happen, inflation always gives the same useless answer: infinity divided by infinity.

The problem is that whatever experiment you make, inflation predicts that there will be infinite copies of you obtaining each physically possible outcome in an infinite number of parallel universes, and despite years of tooth-grinding in the cosmology community, no consensus has emerged on how to extract sensible answers from these infinities. So strictly speaking, we physicists are no longer able to predict anything at all! Our baby universe has grown into an unpredictable teenager.

This is so bad that I think a radical new idea is needed. Perhaps we need to somehow get rid of the infinite. Perhaps, like a rubber band, space can't be expanded ad infinitum without undergoing a big snap? Perhaps those infinite parallel universes get destroyed by some yet undiscovered process, or perchance they're for some reason mere mirages? The very deepest explanations don't just provide answers, but also questions. I think inflation still has some explaining left to do!

Everything Is The Way It Is Because It Got That Way

There is no denying that the central concept of modern biology is evolution, but I'm afraid I was a victim of the American public school system, and I went through twelve years of education without once hearing any mention of the 'controversial' E word. We dissected cats, we memorized globs of taxonomy, we regurgitated extremely elementary fragments of biochemistry on exams, but we were not given any framework to make sense of it all (one reason I care very much about science education now is that mine was so poor).

The situation wasn't much better in college. There, evolution was universally assumed, but there was no remedial introduction to the topic—it was sink or swim, and determined not to drown, I sought out context, anything that would help me understand all these facts my instructors expected me to know. I found it in a used bookstore, a book that I selected because it wasn't too thick and daunting, and because when I skimmed it, it was clearly written, unlike all the massive dense and opaque reference books my classes foisted on me. It was John Tyler Bonner's On Development: The Biology of Form, and it blew my mind, and also warped me permanently to see biology through the lens of development.

The first thing the book taught me wasn't an explanation, which was something of a relief; my classes were just full of explanations already. Bonner's book is about questions, good questions, some of which had answers and others are just hanging there ripely. For instance, how is biological form defined by genetics? It's the implicit question in the title, but the book just refined the questions that we need to answer in order to explain the problem! Or maybe that is an important explanation at a different level; science isn't the body of facts archived in our books and papers, it's the path we follow to acquire new knowledge.

Bonner also led me to D'Arcy Wentworth Thompson and his classic book, On Growth and Form, which provided my favorite aphorism for a scientific view of the universe, "Everything is the way it is because it got that way"—it's a subtle way of emphasizing the importance of process and history in understanding why everything is the way it is. You simply cannot grasp the concepts of science if your approach is to dissect the details in a static snapshot of its current state; your only hope is to understand the underlying mechanisms that generate that state, and how it came to be. The necessity of that understanding is implicit in developmental biology, where all we do is study the process of change in the developing embryo, but I also found it essential as well in genetics, comparative physiology, anatomy, biochemistry...and of course, it is paramount in evolutionary biology.

So my most fundamental explanation is a mode of thinking: to understand how something works, you must first understand how it got that way.

Why The Sun Still Shines

One of the deepest explanations has to be why the sun still shines—and thus why the sun has not long since burned out as do the fires of everyday life. That had to worry some of the sun gazers of old as they watched campfires and forest fires burn through their life cycles. It worried the nineteenth-century scientists who knew that gravity alone could not account for the likely long life of the sun.

It sure worried me when I first thought about it as a child.

The explanation of hydrogen atoms fusing into helium was little comfort. It came at the height of the duck-and-cover cold-war paranoia in the early 1960s after my father had built part of the basement of our new house into a nuclear bomb shelter. The one-room shelter came complete with reinforced concrete and metal windows and a deep freeze packed with homemade TV dinners.

The sun burned so long and so brightly because there were in effect so many mushroom-cloud producing thermonuclear hydrogen-bomb explosions going off inside it and because there was so much hydrogen bomb-making material in the sun. The explosions were just like the hydrogen-bomb explosions that could scorch the earth and that could even incinerate the little bomb shelter if they went off close enough.

The logic of the explanation went well beyond explaining the strategic equilibrium of a nuclear Mexican standoff on a global scale. The good news that the sun would not burn out anytime soon came with the bad news that the sun would certainly burn out in a few billion years. But first it would engulf the molten earth in its red-giant phase.

The same explanation said further that in cosmic due course all the stars would burn out or blow up. There is no free lunch in the heat and light that results when simpler atoms fuse into slightly more complex atoms and when mass transforms into energy. There would not even be stars for long. The universe will go dark and get ever closer to absolute-zero cold. The result will be a faint white noise of sparse energy and matter. Even the black holes will over eons burn out or leak out into the near nothingness of an almost perfect faint white noise. That steady-state white noise will have effectively zero information content. It will be the last few steps in a staggeringly long sequence of irreversible nonlinear steps or processes that make up the evolution of the universe. So there will be no way to figure out the lives and worlds that preceded it even if something arose that could figure.

The explanation of why the sun still shines is deep as it gets. It explains doomsday.

Fooled By Habits

"Caron non ti crucciare: Vuolsi così colà dove si puote ciò che si vuole, e più non dimandare" ("Charon, do not torment yourself: It is so willed where will and power are one, and ask no more") says Virgil to old Charon, justifiably alarmed by the mortal Dante and his inflated sense of entitlement in attempting to cross the Acheron. And so with that explanation they go on, Virgil and his literary pupil in tow. Or rather they would if Dante didn't decide to faint right there and then, as so often happens during his journey through the great poem.

Explanations are seldom as effective as Virgil's, although arguably they can be somewhat more scientific.I suppose I could have chosen any number of elegant scientific theories, but in truth it is a practitioner's explanation rather than that of a theorist, that I find most compelling. My preferred explanation is actually this: that our own habits tend to distort our perception of our own body and its movement.

Have you ever recorded your own voice, listened to it, and wondered how on earth you never realized you sounded like that? Well, the same is true for movement. Often we don't move the way we think we do.

Start by asking someone some basic questions about their anatomy. For example, ask them where is the joint that attaches their arm to the rest of their skeleton. They will likely point to their shoulder. But, functionally, the clavicle—the "collar bone"—is part of the arm and can move with it. In that sense the arm attaches to the rest of the skeleton at the top of the sternum. Ask them to point to the top of their spine, where their head sits. They will likely indicate some point in the middle of their neck. But the top of the first vertebra, the atlas, actually sits more or less at the height of the tip of their nose or the middle of the ear.

The problem is not just having the wrong mental picture of one's anatomy: the problem is being in the habit of moving as if it that were the right one. As it turns out, most of the time we operate our bodies much in the same way that someone without a driving license would operate a car: with difficulty and often hurting ourselves in the process.

One of the people who famously made this observation was a somewhat eccentric Tasmanian actor by the name of F. M. Alexander, around the turn of the last century. Alexander was essentially an empiricist. The story goes that he lost his voice while reciting Shakespeare. After visiting a number of specialists, who could not figure out what in the world was wrong with him, he eventually concluded that the problem must be something he was doing.

What followed was an impressive exercise in solipsistic sublimation: Alexander spent three years observing himself in a three-way mirror, trying to find out what was wrong. Finally he noticed something: When he would declaim verse, he had an almost imperceptible habit of tensing the back of his neck. Could that small tension, unnoticed up to then, possibly explain the loss of voice? It turned out that it did. Alexander continued to observe and explore, and through this process learnt to recognize and retrain his own movement and the use of his body. His voice returned.

To be fair, the study of the body and its movement has a long and illustrious history, from Muybridge onwards. But the realization that our own perception of it may be inaccurate has practical implications that run deep into our capacity to express ourselves.

This point is familiar to performing artists. Playing the key of a piano requires applying a pressure equivalent to about seventy grams, an almost insignificant weight for a human body a thousand times that. Yet most pianists know well the physical exhaustion that can come with playing. Not only their movement fails to achieve efficiency or effectiveness, but it often does not even reflect what they believe to be doing. Not surprisingly, a substantial part of modern piano training consists of inhibiting habitual behavior, in the hopes of achieving Rubinstein's famous effortlessness.

Musicians are not the only ones for whom the idea of retraining one's proprioception is important. For example, our posture and movement communicate plenty of information to those who see us. When wanting to "stand tall", we push our chests out, lift our chin and face. But we fail to notice that this results in a contraction of the neck muscles and therefore a significant shortening of the back, achieving exactly the opposite result. Actors know this well, and have a long tradition of studying the use of the body, recognizing and inhibiting such habits: you cannot control what to communicate through your posture and movement, if you are already busy communicating existing habits. This insight is, alas, true for most of us.

We are fascinated by the natural world as conceptualized in our elegant explanations, yet the single thing we spend the most time doing—using our body—is rarely the subject of extensive analytical consideration. Simple insights of practitioners like Alexander have depth and meaning because they remind us that analytical observation can tell us a lot, not just about the extraordinary, but also about the ordinary in our daily lives.

The True Rotational Symmetry of Space

The following deep, elegant, and beautiful explanation of the true rotational symmetry of space comes from the late Sidney Coleman, as presented to his graduate physics class at Harvard. This explanation takes the form of a physical act that you will perform yourself. Although elegant, this explanation is verbally awkward to explain, and physically awkward to perform. It may need to be practised a few times. So limber up and get ready: you are about to experience in a deep and personal way the true rotational symmetry of space!

At bottom, the laws of physics are based on symmetries, and the rotational symmetry of space is one of the most profound of these symmetries. The most rotationally symmetric object is a sphere. So take a sphere such as a soccer—or basket-ball that has a mark, logo, or unique lettering at some spot on the sphere. Rotate the sphere about any axis: the rotational symmetry of space implies that the shape of the sphere is invariant under rotation. In addition, if there is a mark on the sphere, then when you rotate the sphere by three hundred and sixty degrees, the mark returns to its initial position. Go ahead. Try it. Hold the ball in both hands and rotate it by three hundred and sixty degrees until the mark returns.

That's not so awkward, you may say. But that's because you have not yet demonstrated the true rotational symmetry of space. To demonstrate this symmetry requires fancier moves. Now hold the ball cupped in one hand, palm facing up. Your goal is to rotate the sphere while always keeping your palm facing up. This is trickier, but if Michael Jordan can do it, so can you.

The steps are as follows:

Keeping your palm facing up, rotate the ball inward towards your body. At ninety degrees—one quarter of a full rotation—the ball is comfortably tucked under your arm.

Keep on rotating in the same direction, palm facing up. At one hundred and eighty degrees—half a rotation—your arm sticks out in back of your body to keep the ball cupped in your palm.

As you keep rotating to two hundred and seventy degrees—three quarters of a rotation—in order to maintain your palm facing up, your arm sticks awkwardly out to the side, ball precariously perched on top.

At this point, you may feel that it is impossible to rotate the last ninety degrees to complete one full rotation. If you try, however, you will find that you can continue rotating the ball keeping your palm up by raising your upper arm and bending your elbow so that your forearm sticks straight forward. The ball has now rotated by three hundred and sixty degrees—one full rotation. If you've done everything right, however, your arm should be crooked in a maximally painful and awkward position.

To relieve the pain, continue rotating by an additional ninety degrees to one and a quarter turns, palm up all the time. The ball should now be hovering over your head, and the painful tension in your shoulder should be somewhat lessened.

Finally, like a waiter presenting a tray containing the pi'ece de resistance, continue the motion for the final three quarters of a turn, ending with the ball and your arm—what a relief—back in its original position.

If you have managed to perform these steps correctly and without personal damage, you will find that the trajectory of the ball has traced out a kind of twisty figure eight or infinity sign in space, and has rotated around not once but twice. The true symmetry of space is not rotation by three hundred and sixty degrees, but by seven hundred and twenty degrees!

Although this excercise might seem no more than some fancy and painful basketball move, the fact that the true symmetry of space is rotation not once but twice has profound consequences for the nature of the physical world at its most microscopic level. It implies that 'balls' such as electrons, attached to a distant point by a flexible and deformable 'strings,' such as magnetic field lines, must be rotated around twice to return to their original configuration. Digging deeper, the two-fold rotational nature of spherical symmetry implies that two electrons, both spinning in the same direction, cannot be placed in the same place at the same time. This exclusion principle in turn underlies the stability of matter. If the true symmetry of space were rotating around only once, then all the atoms of your body would collapse into nothingness in a tiny fraction of a second. Fortunately, however, the true symmetry of space consists of rotating around twice, and your atoms are stable, a fact that should console you as you ice your shoulder.

My Favorite Explanation: Why Curry, Wine And Coffee Cure Most Ails

What makes an explanation beautiful? Many elegant explanations in science are those that have been vetted fully but there are just as many beautiful wildly popular explanations where the beauty is just skin deep. I want to give two examples from the field of brain health.

When preliminary mice studies showed that an ingredient in dietary curry spice may have anti-Alzheimer effects, I suspect every vindaloo lover thought that was a beautiful explanation for why India had a low rate of Alzheimer's. But does India really have a low Alzheimer's rate after adjusting for life span and genetic differences? No one really knows.

Likewise when an observational study in the 1990s reported wine drinkers in Bordeaux had lower rates of Alzheimer's, there was a collective "I knew it" from oenophiles.

The latest observational findings now link coffee drinking with lower risk for Alzheimer's, much to the delight of the millions of caffeine addicts.

In reality, neither coffee nor wine nor curry spice have been proven in controlled trials to have any benefits against Alzheimer's. Regardless, the cognitive resonance these "remedies" find with the reader far exceeds the available evidence. One can find similar examples in virtually every field of medicine and science.

I would like to suggest two conditions that might render an explanation unusually beautiful: 1) a ring of truth, 2) confirmation biases. We all favor explanations and test them in a manner that confirms our own beliefs (confirmation bias). A small amount of factual data can be magnified into a beautiful fully proven explanation in one's mind if the right circumstance exist—thus, beauty is in the eye of the beholder. This may occur less often in one's own specialized fields, but we are all vulnerable in fields in which we are less expert in.

Given how often leading scientific explanations are proven wrong in subsequent years, one would do well to bear in mind Santayana's quote that "almost every wise saying has an opposite one, no less wise, to balance it". As for me, I love my curry, coffee and wine but am not yet counting on them to stop Alzheimer's. 

Why Programs Have Bugs

From the earliest days of computer programming up through the present, we are faced with the unfortunate reality that the field does not know how to design error-free programs.

Why can't we tame the writing of computer programs to emulate the successes of other areas of engineering? Perhaps the most lyrical thinker to address this question is Fred Brooks, author most famously of the "The Mythical Man-Month."(If one bears in mind that this unfortunately titled book was first published in 1975, it is a bit easier to ignore the sexist language that litters this otherwise fine work; the points Brooks made more than 35 years ago are almost all accurate today except the assumption that all programmers are "he".)

When espousing the joys of programming, Brooks writes:

"The programmer, like the poet, works only slightly removed from pure thought-stuff. He builds his castles in the air, from air, creating by exertion of the imagination. Few media of creation are so flexible, so easy to polish and rework, so readily capable of realizing grand conceptual structures. ... Yet the program construct, unlike the poet's words, is real in the sense that it moves and works, producing visible outputs separate from the construct itself. It prints results, draws pictures, produces sounds, moves arms. The magic of myth and legend has come true in our time."

But this magic comes with the bite of its flip side:

"In many creative activities the medium of execution is intractable. Lumber splits; paints smear; electrical circuits ring. These physical limitations of the medium constrain the ideas that may be expressed, and they also create unexpected difficulties in the implementation.

... Computer programming, however, creates with an exceedingly tractable medium. The programmer builds from pure thought-stuff: concepts and very flexible representations thereof. Because the medium is tractable, we expect few difficulties in implementation; hence our pervasive optimism. Because our ideas are faulty, we have bugs; henour optimism is unjustified."

Just as there is an arbitrarily large number of ways to arrange the words in an essay, a staggering variety of different programs can be written to perform the same function. The universe of possibility is too wide open, too unconstrained, to permit elimination of errors.

There are additional compelling causes of programming errors, most importantly the complexiting of autonomously interacting independent systems with unpredictable inputs, often driven by even more unpredictable human actions interconnected on a world wide network. But in my view the beautfiul explanation is the one about unfettered thought-stuff.

Beautiful, Unreasonable Mathematics

I find most beautiful not a particular equation or explanation, but the astounding fact that we have beauty and precision in science at all. That exactness comes from using mathematics to measure, check and even predict events. The deepest question is, why does this splendor work?

Beauty is everywhere in science. Physics abounds in symmetries and lovely curves, like the parabola we see in the path of a thrown ball. Equations like e^iΠ+ 1 =0 show that there is exquisite order in mathematics, too.

Why does such beauty exist? That, too, has a beautiful explanation. This may be the most beautiful fact in science.

In 1960, Eugene Wigner published a classic article on the philosophy of physics and mathematics, "The Unreasonable Effectiveness of Mathematics in the Natural Sciences." Wigner asked, why does mathematics work so well in describing our world? He was unsure.

We use Hilbert spaces in quantum mechanics, differential geometry in general relativity, and in biology difference equations and complex statistics. The role mathematics plays in these theories is also varied. Math both helps with empirical predictions and gives us elegant, economical statements of theories. I can't imagine how we could ever invent quantum mechanics or general relativity without it.

But why is this true? For beautiful reasons? I think so.

Darwin stated his theory of natural selection without mathematics at all, but it can explain why math works for us. It has always seemed to me that evolutionary mechanisms should select for living forms that respond to nature's underlying simplicities. Of course, it is difficult to know in general just what simple patterns the universe has. In a sense they may be like Plato's perfect forms, the geometric constructions such as the circle and polygons. Supposedly we see their abstract perfection with our mind's eye, but the actual world only approximately realizes them. Thinking further in like fashion, we can sense simple, elegant ways to viewing dynamical systems. Here's why that matters.

Imagine a primate ancestor who saw the flight of a stone, thrown after fleeing prey, as a complicated matter, hard to predict. It could try a hunting strategy using stones or even spears, but with limited success, because complicated curves are hard to understand. A cousin who saw in the stone's flight a simple and graceful parabola would have a better chance of predicting where it would fall. The cousin would eat more often and presumably reproduce more as well. Neural wiring could reinforce this behavior by instilling a sense of genuine pleasure at the sight of an artful parabola.

There's a further selection at work, too. To hit running prey, it's no good to ponder the problem for long. Speed drove selection: that primate had to see the beauty fast. This drove cognitive capacities all the harder. Plus, the pleasure of a full belly.

We descend from that appreciative cousin. Baseball outfielders learn to sense a ball's deviations from its parabolic descent, due to air friction and wind, because they are building on mental processing machinery finely tuned to the parabola problem. Other appreciations of natural geometric ordering could emerge from hunting maneuvers on flat plains, from the clever design of simple tools, and the like. We all share an appreciation for the beauty of simplicity, a sense emerging from our origins. Simplicity is evolution's way of saying, this works.

Evolution has primed humans to think mathematicallybecause they struggled to make sense of their world for selective advantage. Those who didn't aren't in our genome.

Many things in nature, inanimate and living, show bilateral, radial, concentric and other mathematically based symmetries. Our rectangular houses, football fields and books spring from engineering constraints, their beauty arising from necessity. We appreciate the curve of a suspension bridge, intuitively sensing the urgencies of gravity and tension.

Our cultures show this. Radial symmetry appears in the mandala patterns of almost every society, from Gothic stoneworks to Chinese rugs. Maybe they echo the sun's glare flattened into two dimensions. In all cultures, small flaws in strict symmetries express artful creativity. So do symmetry breaking particle theories.

Philosophers have three views of the issue: mathematics is objective and real; it arises from our preconceptions; or it is social.   

Physicist Max Tegmark argues the first view, that math so well describes the physical world because reality really is completely mathematical. This radical Platonism says that reality is isomorphic to a mathematical structure. We're just uncovering this bit by bit. I hold the second view: we evolved mathematics because it describes the world and promotes survival. I differ from Tegmark because I don't think mathematics somehow generated reality; as Hawking says, what gives fire to the equations, and makes them construct reality?

Social determinists, the third view, think math emerges by consensus. This is true in that we're social animals, but this view also seems to ignore biology, which brought about humans themselves through evolution. Biology generates society, after all.

But how general were our adaptations to our world?

R. Lemarchand and Jon Lomberg have argued in detail that symmetries and other aesthetic principles should be truly universal, because they arise from fundamental physical properties. Aliens orbiting distant stars will still spring from evolutionary forces that reward a deep, automatic understanding of the laws of mechanics. The universe itself began with a Big Bang that can be envisioned as a four-dimensional symmetric expansion; yet without some flaws, so-called anisotropies, in the symmetry of the Big Bang, galaxies and stars would never happen.

Strategies for the Search for Extra-Terrestrial Intelligence, SETI, have assumed this since their beginnings in the early 1960s. Many supposed that interesting properties such as the prime numbers, which do not appear in nature, would figure in schemes to send messages by radio. Primes come from thinking about our mathematical constructions of the world, not directly from that world. So they're evidence for a high culture based on studying mathematics.       

A case for the universality of mathematics is in turn an argument for the universality of aesthetic principles: evolution should shape all of us to the general contours of physical reality. The specifics will differ enormously, of course, as a glance at the odd creatures in our fossil record shows.

Einstein once remarked, "How can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality?" But it isn't independent—and that's beautiful.

How Apparent Finality Can Emerge

Darwin, no doubt. The beauty and the simplicity of his explanation is astonishing. I am sure that others have pointed out Darwin as their favorite deep, elegant, beautiful explanation, but I still want to emphasize the general reach of Darwin's central intuition, which goes well beyond the already monumental result of having clarified that we share the same ancestors with all living beings on Earth, and is directly relevant to the very core of the entire scientific enterprise.

Shortly after the ancient greek "physicists" started to develop naturalistic explanations of Nature, a general objection came forward. The objection is well articulated in Plato, for instance in the Phaedon, and especially in Aristotle discussion of the theory of the "causes". Naturalistic explanations rely on what Aristotle called the "the efficient cause", namely past phenomena producing effects. But the world appears to be dominated by phenomena that can be understood in terms of "final causes", namely an "aim" or a "purpose". These are evident in the kingdom of life. We have the mouth "so we can" eat. The importance of this objection cannot be underestimated. It is this objection that brought down ancient naturalism and in the minds of many it is still today the principal source of psychological resistance against a naturalistic understanding of the world.

Darwin has discovered the spectacularly simple mechanism where efficient causes can produce phenomena that appear to be governed by final causes: anytime we have phenomena that can reproduce, the actual phenomena that we observe are those that keep reproducing, and therefore are necessarily those better at reproducing, and we can thus read them in terms of final causes. In other words, a final cause can be effective to understanding the world because it is a shortcut for accounting the past history of a continuing phenomenon.

To be sure, the idea has appeared before. Empedocles discusses the idea that the apparent finality in the living kingdom could be the result of selected randomness, and Aristotle himself in his "Physics" mentions a version of this idea for species ("seeds"). But the times where not yet ripe, and the suggestion was lost in the following religious ages. I think that the resistance against Darwin is not just the difficulty of seeing the power of a spectacularly beautiful explanation: it is the fear of realizing the extraordinary power that such an explanation has in shattering rests of old world views.

"So Much From So Little? Now That Explains A Lot!"

There is a deep fascination I have been carrying with me for decades now, ever since earliest childhood: the interplay between simplicity and complexity.

Unable to express it verbally at the time, in hindsight it seems clear: they are all about that penultimate question: what is life and how did this world come into existence?

In many stages and phases I discovered a multitude of ideas that are exactly what is called for here: deep, elegant and beautiful explanations of the principles of nature.

Simplicity is embodied in a reductionist form in the YinYang symbol: being black or white.

In other familiar words: To be or not to be.

Those basic elements combined: that is the process spawning diversity, in myriads of forms.

As a youngster I was totally immersed in 'Lego' blocks. There are a handful of basic shapes (never liked the 'special' ones and clamored instead for a bigger box of basics) and you could put them together in arrangements that become houses, ships, bridges...entire towns I had growing up the sides of my little room to the tops of wardrobes. And I sensed it then: there is something deep about this.

A bit later I got into a mechanical typewriter (what a relief to be able to type clearly, my handwriting had always been horrid—the hand not being able to keep up with the thinking... and relished the ability to put together words, sentences, paragraphs. Freezing a thought in a material fashion, putting it on paper to recall later. What's more—to let someone else follow your thinking! I sensed: this is a thing of beauty.

Then I took up playing the piano. The embryonic roots of the software designer of later decades probably shuddered at the interface: 88 unlabeled keys! Irregular intervals of black ones interspersed... and almost the exact opposite of todays "we need to learn this in one minute and no, we never ever look at manuals" attitude. It took months to make any sense of it, but despite the frustrations, it was deeply fascinating. String together a few notes with mysterious un-definable skill and out comes... deeply moving emotion?

So the plot thickens: a few Lego blocks, a bunch of lettershapes or a dozen musical notes... and you take that simplicity of utterly lame elements, put them together...and out pops complexity, meaning, beauty.

Later in the early 70s I delved into the very first generation of large synthesizers and dealt specifically with complex natural sounds being generated from simple unnatural ingredients and processes. By 1977—now in California—it was computer graphics that became the new frontier—and again: seemingly innocent little pixels combine to make ... any image—as in: anything one can imagine. Deep.

In those days I also began playing chess, and carom billiards—simple rules, a few pieces, 3 balls...but no game is ever the same. Not even close. The most extreme example of this became another real fascination: the game of GO. Just single moves of black and white stones, on a plain grid of lines with barely a handful of rules—but a huge variety of patterns emerges. Elegant.

The earliest computing, in the first computer store in the world, Dick Heyser in Santa Monica, had me try something that I had read in SciAm by Martin Gardner: Conway's 'Game of Life'. The literal incarnation of the initial premise: Simplicity reduced to that YinYang: a cell is On or Off, black or white. But there is one more thing added here now: iteration. With just four rules each cell is said to live or die and in each cycle the pattern changes, iteratively. From dead dots on paper, and static pixels on phospor, it sprang to—life! Not only patterns, but blinkers, gliders, even glider guns, heck glider gun canons! Indeed, it is now seen as a true Turing-complete machine. Artificial Life. Needless to say: very deep.

Another example in that vein are of course fractals. Half an inch of a formula, when iterated, is yielding worlds of unimaginably intricate shapes and patterns. It was a great circle closing after 20 years for me to re-examine this field, now flying through them as "frax" on a little iPhone, in realtime and in real awe.

The entire concept of the computer embodies the principles of simple on/off binary codes, much like YinYang, being put together to form still simplistic gates and then flip-flops, counters, all the way to RAM and complex CPU/GPUs and beyond. And now we have a huge matrix computer with billions of elements networked together (namely 'us', including this charming little side corridor called 'Edge'), just a little over

70 years after Zuse's Z3 we reached untold complexity—with no sign of slowing down.

Surely the ultimate example of 'simplexity' is the genetic code—four core elements being combined by simple rules to extreme complex effect—the DNA to build archaea, felis or homo somewhat sapiens.

Someone once wrote on Edge "A great analogy is like...a diagonal frog" which embodies the un-definable art of what constitutes a deep, beautiful or elegant explanation: Finding the perfect example! The lifelong encounters with "trivial ingredients turning to true beauty" recited here are in themselves neither terse mathematical proofs nor eloquently worded elucidations (such as one could quote easily from almost any Nobel laureate's prize-worthy insights).

Instead of the grandeur of 'the big formulas' I felt that the potpourri of AHA!  moments over six decades may be just as close to that holy grail of scientific thinking: to put all the puzzle pieces together in such away that a logical conclusion converges further on... the truth. And I guess one of the pillars of that truth, in my eyes, is the charmingly disarmingly miniscule insight:

 "So much from so little. Now that explains a lot!"

An Unresolved (And, Therefore, Unbeautiful) Reaction To The Edge Question

This year's Edge question sits uneasily on a deeper question: Where do we get the idea—a fantastic idea if you stop and think about it—that the beauty of an explanation has anything to do with the likelihood of its being true? What do beauty and truth have to do with each other? Is there any good explanation of why the central notion of aesthetics (fluffy) should be inserted into the central notion of science (rigorous)?

You might think that, rather than being a criterion for assessing explanations, the sense of beauty is a phenomenon to be explained away. Take, for example, our impression that symmetrical faces and bodies are beautiful. Symmetry, it turns out, is a good indicator of health and, consequently, of mate-worthiness. It's a significant challenge for an organism to coordinate the production of its billions of cells so that its two sides proceed to develop as perfect matches, warding off disease and escaping injury, mutation and malnutrition. Symmetrical female breasts, for example, are a good predictor of fertility. As our own lustful genes know, the achievement of symmetry is a sign of genetic robustness, and we find lopsidedness a turnoff. So, too, in regard to other components of human beauty—radiant skin, shining eyes, neotony (at least in women). The upshot is that we don't want to mate with people because they're beautiful, but rather they're beautiful because we want to mate with them, and we want to mate with them because our genes are betting on them as replicators.

So, too, you might think that beauty of every sort is to be similarly explained away, an attention-grabbing epiphenomenon with no substance of its own.  Which brings me to the Edge question concerning beautiful explanations. Is there anything to this notion of explanatory beauty, a guide to choosing between explanatory alternatives, or it just that any explanation that's satisfactory will, for that very reason and no other, strike us as beautiful, beautifully explanatory, so that the reference to beauty is once again without any substance? That would be an explanation for the mysterious injection of aesthetics into science. The upshot would be that explanations aren't satisfying because they're beautiful, but rather they're beautiful because they're satisfying: they strip the phenomenon bare of all mystery, and maybe, as a bonus, pull in further phenomena which can be rendered non-mysterious using the same sort of explanation. Can explanatory beauty be explained away, summarily dismissed by way of an eliminative explanation? (Eliminative explanations are beautiful.)

I'd like to stop here, with a beautiful explanation for explaining away explanatory beauty, but somebody is whispering in my ear. It's that damned Plato. Plato is going on about how there is more in the idea of explanatory beauty than is acknowledged in the eliminative explanation. In particular, he's insisting, as he does in his Timaeus, that the beauty of symmetry, especially as it's expressed in the mathematics of physical laws, cannot be explained away with the legerdemain of the preceding paragraph. He's reproaching the eliminative explanation of explanatory beauty with ignoring the many examples in history when the insistence on the beauty of symmetry led to substantive scientific progress. What was it that led James Clerk Maxwell to his four equations of electromagnetism but his trying to impose mathematical symmetry on the domains of electricity and magnetism? What was it that led Einstein to his equations of gravity but an insistence on beautiful mathematics?

Eliminative explanations are beautiful, but only when they truly and thoroughly explain. So instead of offering an answer to this year's Edge question I offer instead an unresolved (and, therefore, unbeautiful) reaction to the deep question on which it rests.   

The Simpleton Ant and the Intelligent Ants

The obvious answer should be the double helix. With the incomparably laconic "It has not escaped our notice….," it explained the very mechanism of inheritance. But the double helix doesn't do it for me. By the time I got around to high school biology, the double helix was ancient history, like pepper moths evolving or mitochondria as the power houses of the cell. Watson and Crick—as comforting but as taken for granted as Baskin and Robbins.

Then there's the work of Hubel and Wiesel, which showed that the cortex processes sensations with a hierarchy of feature extraction. In the visual cortex, for example, neurons in the initial layer each receive inputs from a single photoreceptor in the retina. Thus, when one photoreceptor is stimulated, so is "its" neuron in the primary visual cortex. Stimulate the adjacent photoreceptor, and the adjacent neuron activates. Basically, each of these neurons "knows" one thing, namely how to recognize a particular dot of light. Groups of I-know-a-dot neurons then project onto single neurons in the second cortical layer. Stimulate a particular array of adjacent neurons in that first cortical layer and a single second layer neuron activates. Thus, a second layer neuron knows one thing, which is how to recognize, say, a 45 degree angle line of light oriented. Then groups of I-know-a-line neurons send projections on to the next layer. 

Beautiful, explains everything—just keep going, cortical layer upon layer of feature extraction, dot to line to curve to collection of curves to…….until there'd be the top layer where a neuron would know one complex, specialized thing only, like how to recognize your grandmother.  And it would be the same in the auditory cortex—first layer neurons knowing particular single notes, second layer knowing pairs of notes….some neuron at the top that would recognize the sound of your grandmother singing along with Lawrence Welk.

It turned out, though, that things didn't quite work this way. There are few "Grandmother neurons" in the cortex (although a 2005 Nature paper reported someone with a Jennifer Aniston neuron). The cortex can't rely too much on grandmother neurons, because that requires a gazillion more neurons to accommodate such inefficiency and overspecialization. Moreover, a world of nothing but grandmother neurons on top precludes making multi-modal associations (e.g., where seeing a particular Monet reminds you of croissants and Debussy's music and the disastrous date you had at an Impressionism show at the Met. Instead, we've entered the world of neural networks.

Switching to a more mundane level of beauty, consider the gastrointestinal tract. In addition to teaching neuroscience, I've been asked to be a good departmental citizen and fill in some teaching holes in our core survey course. Choices: photosynthesis, renal filtration or the gastrointestinal tract. I picked the GI tract, despite knowing nothing about it, since the first two subjects terrified me. Gut physiology turns out to be beautiful and elegant amid a huge number of multi-syllabic hormones and enzymes. As the Gentle Reader knows, the GI tract is essentially a tube starting at the mouth and ending at the anus. When a glop of food distends the tube, the distended area secretes some chemical messenger that causes that part of the tube to start doing something (e.g., contracting rhythmically to pulverize food). But the messenger also causes the part of the tract just behind to stop doing its now-completed task and causes area just ahead to prepare for its job. Like shuttling ships through the Panama Canal's locks, all the way to the bathroom.

Beautiful. But even bowelophiles wouldn't argue that this is deep on a fundamental, universe-explaining level. Which brings me to my selection, which is emergence and complexity, as represented by "swarm intelligence."

Observe a single ant, and it doesn't make much sense, walking in one direction, suddenly careening in another for no obvious reason, doubling back on itself. Thoroughly unpredictable.

The same happens with two ants, a handful of ants. But a colony of ants makes fantastic sense. Specialized jobs, efficient means of exploiting new food sources, complex underground nests with temperature regulated within a few degrees. And critically, there's no blueprint or central source of command—each individual ants has algorithms for their behaviors. But this is not wisdom of the crowd, where a bunch of reasonably informed individuals outperform a single expert. The ants aren't reasonably informed about the big picture. Instead, the behavior algorithms of each ant consist of a few simple rules for interacting with the local environment and local ants. And out of this emerges a highly efficient colony.

Ant colonies excel at generating trails that connect locations in the shortest possible way, accomplished with simple rules about when to lay down a pheromone trail and what to do when encountering someone else's trail—approximations of optimal solutions to the Traveling Salesman problem. This has useful applications. In "ant-based routing," simulations using virtual ants with similar rules can generate optimal ways of connecting the nodes in a network, something of great interest to telecommunications companies. It applies to the developing brain, which must wire up vast numbers of neurons with vaster numbers of connections without constructing millions of miles of connecting axons. And migrating fetal neurons generate an efficient solution with a different version of ant-based routine.

A wonderful example is how local rules about attraction and repulsion (i.e., positive and negative charges) allow simple molecules in an organic soup to occasionally form more complex ones. Life may have originated this way without the requirement of bolts of lightening to catalyze the formation of complex molecules.

And why is self-organization so beautiful to my atheistic self? Because if complex, adaptive systems don't require a blue print, they don't require a blue print maker. If they don't require lightening bolts, they don't require Someone hurtling lightening bolts. 

Embodied Metaphors Unify Perception, Cognition and Action

Philosophers and psychologists grappled with a fundamental question for quite some time: How does the brain derive meaning? If thoughts consist of the manipulation of abstract symbols, just like computers are processing 0s and 1s, then how are such abstract symbols translated into meaningful cognitive representations? This so-called "symbol grounding problem" has now been largely overcome because many findings from cognitive science suggest that the brain does not really translate incoming information into abstract symbols in the first place. Instead, sensory and perceptual inputs from every-day experience are taken in their modality-specific form, and they provide the building blocks of thoughts.

British empiricists such as Locke and Berkeley long ago recognized that cognition is inherently perceptual. But following the cognitive revolution in the 1950ies psychology treated the computer as the most appropriate model to study the mind. Now we know that a brain does not work like a computer. Its job is not to store or process information; instead, its job is to drive and control the actions of the brain's large appendage, the body. A new revolution is taking shape, considered by some to bring an end to cognitivism, and giving way to a transformed kind of cognitive science, namely an embodied cognitive science.

The basic claim is thatthe mind thinks in embodied metaphors. Early proponents of this idea were linguists such as George Lakoff, and in recent years social psychologists have been conducting the relevant experiments, providing compelling evidence. But it does not stop here; there is also a reverse pathway: Because thinking is for doing, many bodily processes feed back into the mind to drive action.

Consider the following recent findings that relate to the very basic spatial concept of verticality. Because moving around in space is a common physical experience, concepts such as "up" or "down" are immediately meaningful relative to one's own body. The concrete experience of verticality serves as a perfect scaffold for comprehending abstract concepts, such as morality: Virtue is up, whereas depravity is down: Good people are "high minded" and "upstanding" citizens, whereas bad people are "underhanded" and the "low life" of society. Recent research by Brian Meier, Martin Sellbom and Dustin Wygant illustrated that research participants are faster to categorize moral words when they are presented in an up location, and immoral words when they are presented in a down location. Thus, people intuitively relate the moral domain to verticality; however, Meier and colleagues also found that peoplewho do not recognize moral norms, namely psychopaths, fail to do so, and do not show this effect.

People not only think of all things good and moral as up, but they also think of God as up, and the Devil as down. Further, those in power are conceptualized as being high up relative to those down below over whom they hover and exert control, as shown by Thomas Schubert.All the empirical evidence suggests that there is indeed a conceptual dimension that leads up, both literally and metaphorically. This vertical dimension that pulls the mind up to considering what higher power there might be is deeply rooted in the very basic physical experience of verticality.

However, verticality not only influences people's representation of what is good, moral and divine, but movement through space along the vertical dimension can even change their moral actions. Larry Sanna, Edward Chang, Paul Miceli and Kristjen Lundberg recently demonstrated that manipulating people's location along the vertical dimension can actually turn them into more "high minded" and "upstanding" citizens. They found that people in a shopping mall who had just moved up an escalator were more likely to contribute to a charity donation box than people who had moved down on the escalator. Similarly, research participants who had watched a film depicting a view from high above, namely flying over clouds seen from an airplane window subsequently showed more cooperative behaviour than participants who had watched a more ordinary, and less "elevating" view from a car window. Thus, being physically elevated induced people to act on "higher" moral values.

The growing recognition that embodied metaphors provide one common language of the mind has lead to fundamentally different ways of studying how people think. For example, under the assumption that the mind functions like a computer psychologists hoped to figure out how people think by observing how they play chess, or memorize lists of random words. From an embodied perspective it is evident that such scientific attempts were hopelessly doomed to fail. Instead, it is increasingly clear that cognitive operations of any creature, including humans, have to solve certain adaptive challenges of the physical environment. In the process, embodied metaphors are the building blocks of perception, cognition, and action. It doesn't get much more simple and elegant than that.

The Double Helix

The Double Helix is a strong candidate. 

"It Just Is?"

The concept of an indivisible component of matter, something that cannot be divided further, has been around for at least two and half millennia, first proposed by early Greek and Indian philosophers. Democritus called the smallest indivisible particle of matter "átomos" meaning "uncuttable". Atoms were also simple, eternal, and unalterable. But in Greek thinking (and generally for about 2,000 years after) atoms lost out to the four basic elements of Empedocles—fire, air, water, earth—which were also simple, eternal, and unalterable, but not made up of little particles, Aristotle believing those four elements to be infinitely continuous.

Further progress in our understanding of the world based on the concept of atoms had to wait till the 18^th century. By that time the four elements of Aristotle had been replaced by 33 elements of Lavoisier based on chemical analysis. Dalton then used the concept of atoms to explain why elements always react in ratios of whole numbers, proposing that each element is made up of atoms of a single type, and that these atoms can combine to form chemical compounds. Of course, by the early 20^th century (through the work of Thompson, Rutherford, Bohr and many others) it was realized that atoms were not indivisible and they were thus not the basic units of matter. All atoms were made up of protons, neutrons, and electrons, which took over the title of being the indivisible components (basic building blocks) of matter.

Perhaps because the Rutherford-Bohr model of the atom is now considered transitional to more elaborate models based on quantum mechanics, or perhaps because it evolved over time from the work of many people (and wasn't a single beautiful proposed law), we have forgotten how much about the world can be explained by the concept of protons, neutrons, and electrons—probably more than any other theory ever proposed. With only three basic particles one could explain the properties of 118 atoms/elements and the properties of thousands upon thousands of compounds chemically combined from those elements. A rather amazing feat, and certainly making the Rutherford-Bohr model worthy of being considered a favorite deep, elegant, and beautiful explanation.

Since that great simplification, further developments in our understanding of the physical universe have gotten more complicated, not less. To explain the properties of our three basic particles of matter, we went looking for even-more-basic particles. We ended up needing 12 fermions (6 quarks, 6 leptons) to "explain" the properties of the 3 previously thought-to-be basic particles (as well as the properties of some other particles that were not known to us until we built high energy colliders). And we added 4 other particles, force-carrier particles, to "explain" the 4 basic force fields (electromagnetism, gravitation, strong interaction, and weak interaction) that affect those 3 previously thought-to-be basic particles. Of these 16 now thought-to-be basic particles most are not independently observable (at least at low energies).        

Even if the present Standard Model of particle physics turns out to be true, the question can be asked: "What next?" Every particle (whatever it's level in the hierarchy of particles) will have certain properties or characteristics. When asked "why" quarks have a particular electric charge, color charge, spin, or mass, do we simply say "they just do"? Or do we try to find even-more-basic particles which seem to explain the properties of quarks, and of leptons and bosons? And if so, does this continue on to still-even-more-basic particles? Could that go on forever? Or at some point, when asked the question "why does this particle have these properties", would we simply say "it just does"? At some point would we have to say that there is no "why" to the universe? "It just is."

At what level of our hierarchy of understanding would we resort to saying, "it just is"? The highest (and least understanding) level is religious—the gods of Mount Olympus each responsible for some worldly phenomenon, or the all-knowing monotheistic god creating the world and making everything work by means truly unknowable to humans. In their theories about how the world worked Aristotle and other Greek philosophers incorporated the gods of Mount Olympus (earth, water, fire, and air were all assigned to particular gods), but Democritus and other philosophers were deterministic and materialistic, and they looked for predictable patterns and simple building blocks that might create the complex world they saw around them. Throughout the growth and evolution of scientific thinking there have been various "it just is" moments, where an explanation/theory seems to hit a wall where one might say "it just is", only to have some one else come along and say "maybe not" and goes on to further advance our understanding. But as we get to the most basic questions about our universe (and our existence) the "it just is" answer becomes more likely. One very basic scientific question is whether there will ever be found truly indivisible particles of nature. The accompanying philosophical question is whether there can be truly indivisible particles of nature.

At some level the next group of mathematically derived "particles" may so obviously appear not to be observable/"real", that we will describe them instead as simply entities in a mathematical model that appears to accurately describe the properties of the observable particles in the level above. At which point the answer to the question of why these particles act as described by this mathematical model would be "they just do". How far down we go with such models will probably depend on how much a new level in the model allows us to explain previously unexplainable observed phenomena or to correctly predict new phenomena. (Or perhaps we might be stopped by the model becoming too complex.)

For determinists still unsettled by the probabilities inherent in quantum mechanics or the philosophical question about what would have come before a Big Bang, it is just one more step toward recognizing the true unsolvable mystery of our universe—recognizing it, but maybe still not accepting it; a new much better model could still come along.

The Higgs Mechanism

The beauty of science—in the long run—is its lack of subjectivity. So answering the question "what is your favorite deep, beautiful, or elegant explanation" can be a little disturbing to a scientist, since the only objective words in the question are "what", "is", "or", and (in an ideal scientific world) "explanation." Beauty and elegance do play a part in science but are not the arbiters of truth. But I will admit that simplicity, which is often confused with elegance, can be a useful guide to maximizing explanatory power.

As for the question, I'll stick to an explanation that I think is extremely nice, relatively simple (though subtle), and which might even be verified within the year. That is the Higgs mechanism, named after the physicist Peter Higgs who developed it. The Higgs mechanism is probably responsible for the masses of elementary particles like the electron. If the electron had zero mass (like the photon), it wouldn't be bound into atoms. If that were the case, none of the structure of our Universe (or of life) would be present. That's not the correct description of our world.

 In any case, experiments have measured the masses of elementary particles and they don't vanish. We know they exist. The problem is that these masses violate the underlying symmetry structure we know to be present in the physical description of these particles. More concretely, if elementary particles had mass from the get-go, the theory would make ridiculous predictions about very energetic particles. For example, it would predict interaction probabilities greater than one.

So there is a significant puzzle. How can particles have masses that have physical consequences and can be measured at low energies but act as if they don't have masses at high energies, when predictions would become nonsensical? That is what the Higgs mechanism tells us. We don't yet know for certain that it is indeed responsible for the origin of elementary particle masses but no one has found an alternative satisfactory explanation.

One way to understand the Higgs mechanism is in terms of what is known as "spontaneous symmetry breaking," which I'd say is itself a beautiful idea. A spontaneously broken symmetry is broken by the actual state of nature but not by the physical laws. For example, if you sit at a dinner table and use your glass on the right, so will everyone else. The dinner table is symmetrical—you have a glass on your right and also to your left. Yet everyone chooses the glass on the right and thereby spontaneously breaks the left-right symmetry that would otherwise be present.

Nature does something similar. The physical laws describing an object called a Higgs field respects the symmetry of nature. Yet the actual state of the Higgs field breaks the symmetry. At low energy, it takes a particular value. This nonvanishing Higgs field is somewhat akin to a charge is spread throughout the vacuum (the state of the universe with no actual particles). Particles acquire their masses by interacting with these "charges." Because this value appears only at low energies, particles effectively have masses only at these energies and the apparent bottleneck to elementary particle masses is apparently resolved.

Keep in mind that the Standard Model has worked extremely well, even without yet knowing for sure if the Higgs mechanism is correct. We don't need to know about the Higgs mechanism to know particles have masses and to make many successful predictions with the so-called Standard Model of particle physics. But the Higgs mechanism is essential to explaining how those masses can arise in a sensible theory. So it is rather significant.

The Standard Model's success nonetheless illustrates another beautiful idea essential to all of physics, which is the concept of an "effective theory." The idea is simply that you can focus on measurable quantities when making predictions and leave understanding the source of those quantities to later research when you have better precision.

Fortunately that time has now come for the Higgs mechanism, or at least the simplest implementation which involves a particle called the Higgs boson. The Large Hadron Collider at CERN near Geneva should have a definitive result on whether this particle exists within this coming year. The Higgs boson is one possible (and many think the most likely) consequence of the Higgs mechanism. Evidence last December pointed to a possible discovery, though more data is needed to know for sure. If confirmed, it will demonstrate that the Higgs mechanism is correct and furthermore tell us what is the underlying structure responsible for spontaneous symmetry breaking and spreading "charge" throughout the vacuum. The Higgs boson would furthermore be a new type of particle (a fundamental boson for those versed in physics terminology) and would be in some sense a new type of force. Admittedly, this is all pretty subtle and esoteric. Yet I (and much of the theoretical physics community) find it beautiful, deep, and elegant.

Symmetry is great. But so is symmetry breaking. Over the years many aspects of particle physics were first considered ugly and then considered elegant. Subjectivity in science goes beyond communities to individual scientists. And even those scientists change their minds over time. That's why experiments are critical. As difficult as they are, results are much easier to pin down than the nature of beauty. A discovery of the Higgs boson will tell us how that is done when particles acquire their masses.

Continuity

For me, the answer to this year's Edge question is clear: The Continuity Equations.

These are already familiar to you, at least in anecdotal form. Most everyone has heard of the law of "Conservation of Mass" (sometimes using the word "matter" instead of mass) and probably its partner "Conservation of Energy" too. These laws tell us that for practical, real-world (i.e. non-quantum, non-general relativity) phenomena, matter and energy can never be created or destroyed, only shuffled around. That concept has origins tracing at least as far back as the ancient Greeks, was formally articulated in the 18^th century (a major advance for modern chemistry), and today underpins virtually every aspect of the physical, life, and natural sciences. Conservation of Mass (matter) is what finally quashed the alchemists' quest to transform lead to gold; Conservation of Energy is what consigns the awesome power of a wizard's staff to the imaginations of legions of Lord of the Rings fans.

The Continuity Equations take these laws an important step further, by providing explicit mathematical formulations that track the storage and/or transfers of mass (Mass Continuity) and energy (Energy Continuity) from one compartment or state to another. As such, they are not really a single pair of equations but instead written into a variety of forms, ranging from the very simple to the very complex, in order to best represent the physical/life science/natural world phenomenon they are supposed to describe. The most elegant forms, adored by mathematicians and physicists, have exquisite detail and are therefore the most complex. A classic example is the set of Navier-Stokes equations (sometimes called the Saint-Venant equations) used to understand the movements and accelerations of fluids. The beauty of Navier-Stokes lies in their explicit partitioning and tracking of mass, energy and momentum through space and time. However, in practice such detail also makes them difficult to solve, requiring either hefty computing power or simplifying assumptions to be made to the equations themselves.

But the power of the Continuity Equations is not limited to complex forms comprehensible solely to mathematicians and physicists. A forest manager, for example, might use a simple, so-called "mass balance" form of a mass continuity equation to study her forest, by adding up the number, size, and density of trees, the rate at which seedlings establish, and subtracting the trees' mortality rate and number of truckloads of timber removed to learn if its total wood content (biomass) is increasing, decreasing, or stable. Automotive engineers routinely apply simple "energy balance" equations when, for example, designing a hybrid electric car to recapture kinetic energy from its braking system. None of the energy is truly created or destroyed just recaptured (e.g. from a combustion engine, which got it from breaking apart ancient chemical bonds, which got it from photosynthetic reactions, which got it from the Sun). Any remaining energy not recaptured from the brakes is not really "lost", of course, but instead transferred to the atmosphere as low-grade heat.

The cardinal assumption behind these laws and equations is that mass and energy are conserved (constant) within a closed system. In principle, the hybrid electric car only satisfies energy continuity if its consumption is tracked from start (the Sun) to finish (dissipation of heat into the atmosphere). This a bit cumbersome so it is usually treated as an open system. The metals used in the car's manufacture satisfy mass continuity only if tracked from their source (ores) to landfill. This is more feasible, and such "cradle-to-grave" resource accounting—a high priority for many environmentalists—is thus more compatible with natural laws than our current economic model, which tends to externalize (i.e., assume an open system) such resource flows.

Like the car, our planet, from a practical standpoint, is an open system with respect to energy and a closed system with respect to mass (while it's true that Earth is still being bombarded by meteorites, that input is now small enough to be neglected). The former is what makes life possible: Without the Sun's steady infusion of fresh, external energy, life as we know it would quickly end. An external source is required because although energy cannot be destroyed, it is constantly degraded into weaker, less useful forms in accordance with the 2^nd law of thermodynamics (consider again the hybrid-electric car's brake pads—their dissipated heat is of not much use to anyone). The openness of this system is two-way, because Earth also streams thermal infrared energy back out to space.  Its radiation is invisible to us, but to satellites with "vision" in this range of the electromagnetic spectrum the Earth is a brightly glowing orb, much like the Sun.  

Interestingly, this closed/open dichotomy is yet another reason why the physics of climate change are unassailable. By burning fossil fuels, we shuffle carbon (mass) out of the subsurface—where it has virtually no interaction with the planet's energy balance—to the atmosphere, where it does. It is well understood that carbon in the atmosphere alters the planet's energy balance (the physics of this have been known since 1893) and without carbon-based and other greenhouse gases our planet would be a moribund, ice-covered rock. Greenhouse gases prevent this by selectively altering the Earth's energy balance in the troposphere (the lowest few miles of the atmosphere, where the vast majority of its gases reside), thus raising the amount of thermal infrared radiation that it emits. Because some of this energy streams back down to Earth (as well as out to space) the lower troposphere warms, to achieve energy balance. Continuity of Energy commands this.

Our planet's carbon atoms, however, are stuck here with us forever—Continuity of Mass commands that too. The real question is what choices will make about how much, and how fast, to shuffle them out the ground. The physics of natural resource stocks, climate change and other problems can often be reduced to simple, elegant, equations—if only we had such masterful tools to dictate their solution.

Cosmic Complexity

What explains the extraordinary complexity of the observed universe, on all scales from quarks to the accelerating universe? My favorite explanation (which I certainly did not invent) is that the fundamental laws of physics produce natural instability, energy flows, and chaos. Some call the result the Life Force, some note that the Earth is a living system itself (Gaia, a "tough bitch" according to Margulis), and some conclude that the observed complexity requires a supernatural explanation (of which we have many). But my dad was a statistician (of dairy cows) and he told me about cells and genes and evolution and chance when I was very small. So a scientist must look for the explanation of how nature's laws and statistics brought us into conscious existence. And how is that seemingly improbable events are actually happening all the time?

Well, the physicists have countless examples of natural instability, in which energy is released to power change from simplicity to complexity. One of the most common to see is that cooling water vapor below the freezing point produces snowflakes, no two alike, and all complex and beautiful. We see it often so we are not amazed. But physicists have observed so many kinds of these changes from one structure to another (we call them phase transitions) that the Nobel Prize in 1992 could be awarded for understanding the mathematics of their common features.

Now for a few examples of how the laws of nature produce the instabilities that lead to our own existence. First, the Big Bang (what an insufficient name!) apparently came from an instability, in which the "false vacuum" eventually decayed into the ordinary vacuum we have today, plus the most fundamental particles we know, the quarks and leptons. So the universe as a whole started with an instability. Then, a great expansion and cooling happened, and the loose quarks, finding themselves unstable too, bound themselves together into today's less elementary particles like protons and neutrons, liberating a little energy and creating complexity. Then, the expanding universe cooled some more, and neutrons and protons, no longer kept apart by immense temperatures, found themselves unstable and formed helium nuclei. Then, a little more cooling, and atomic nuclei and electrons were no longer kept apart, and the universe became transparent. Then a little more cooling, and the next instability began: gravitation pulled matter together across cosmic distances to form stars and galaxies. This instability is described as a "negative heat capacity" in which extracting energy from a gravitating system makes it hotter—clearly the 2^nd law of thermodynamics does not apply here! (This is the physicist's part of the answer to e e cummings' question: what is the wonder that's keeping the stars apart?) Then, the next instability is that hydrogen and helium nuclei can fuse together to release energy and make stars burn for billions of years. And then at the end of the fuel source, stars become unstable and explode and liberate the chemical elements back into space. And because of that, on planets like Earth, sustained energy flows support the development of additional instabilities and all kinds of complex patterns. Gravitational instability pulls the densest materials into the core of the Earth, leaving a thin skin of water and air, and makes the interior churn incessantly as heat flows outwards. And the heat from the Sun, received mostly near the equator and flowing towards the poles, supports the complex atmospheric and oceanic circulations.

And because of that, the physical Earth is full of natural chemical laboratories, concentrating elements here, mixing them there, raising and lowering temperatures, ceaselessly experimenting with uncountable events where new instabilities can arise. At least one of them was the new experiment called Life. Now that we know that there are at least as many planets as there are stars, it is hard to imagine that nature's ceaseless experimentation would not be able to produce Life elsewhere—but we don't know for sure.

And Life went on to cause new instabilities, constantly evolving, with living things in an extraordinary range of environments, changing the global environment, with boom-and-bust cycles, with predators for every kind of prey, with criminals for every possible crime, with governments to prevent them, and instabilities of the governments themselves.

One of the instabilities is that humans demand new weapons and new products of all sort, leading to serious investments in science and technology. So the natural/human world of competition and combat is structured to lead to advanced weaponry and cell phones. So here we are in 2012, with people writing essays and wondering whether their descendents will be artificial life forms travelling back into space. And, pondering what are the origins of those forces of nature that give rise to everything. Verlinde has argued that gravitation, the one force that has so far resisted our efforts at a quantum description, is not even a fundamental force, but is itself a statistical force, like osmosis.

What an amazing turn of events! But after all I've just said, I should not be surprised a bit.

Personality Differences: The Importance of Chance

In the golden age of Greek philosophy Theophrastus, Aristotle's successor, posed a question for which he is still remembered: "Why has it come about that, albeit the whole of Greece lies in the same clime, and all Greeks have a like upbringing, we have not the same constitution of character [personality]?" The question is especially noteworthy because it bears on our sense of who each of us is, and we now know enough to offer an answer: each personality reflects the activities of brain circuits that gradually develop under the combined direction of the person's unique set of genes and experiences. What makes the implications of this answer so profound is that they lead to the inescapable conclusion that personality differences are greatly influenced by chance events.

Two types of chance events influence the genetic contribution to personality. The first, and most obvious, is the events that brought together the person's mom and dad. Each of them has a particular collection of gene variants—a personal sample of the variants that have accumulated in the collective human genome—and the two parental genetic repertoires set limits on the possible variants that can be transmitted to their offspring. The second chance event is the hit-or-miss union of the particular egg and sperm that make the offspring, each of which contains a random selection of half of the gene variants of each parent. It is the interactions of the resultant unique mixture of maternal and paternal gene variants that plays a major part in the 25-year-long developmental process that builds the person's brain and personality. So two accidents of birth—the parents who conceive us, and the egg–sperm combinations that make us—have decisive influences on the kinds of people we become.

But genes don't act alone. Although there are innate programs of gene expression that continue to unfold through early adulthood to direct the construction of rough drafts of brain circuits, these programs are specifically designed to incorporate information from the person's physical and social world. Some of this adaptation to the person's particular circumstances must come at specific developmental periods, called critical periods. For example, the brain circuits that control the characteristic intonations of a person's native language are only open for environmental input during a limited window of development.

And just as chance influences the particular set of genes we are born with, so does it influence the particular environment we are born into. Just as our genes incline us to be more or less friendly, or confident, or reliable, the worlds we grow up in incline us to adopt particular goals, opportunities and rules of conduct. The most obvious aspects of these worlds are cultural, religious, social, and economic, each transmitted by critical agents: parents, siblings, teachers, and peers. And the specific content of these important influences—the specific era, place, culture etc. we happen to have been born into—is as much a toss of the dice as the specific content of the egg and sperm that formed us.

Of course, chance is not fate. Recognizing that chance events contribute to individual personality differences doesn't mean each life is predetermined or that there is no free will. The personality that arises through biological and socio-cultural accidents of birth can be deliberately modified in many ways, even in maturity. Nevertheless, the chance events that direct brain development in our first few decades leave enduring residues.

When thinking about a particular personality it is, therefore, helpful to be aware of the powerful role that chance played in its construction. Recognizing the importance of chance in our individual differences doesn't just remove some of their mystery. It can also have moral consequences by promoting understanding and compassion for the wide range of people with whom we share our lives.

Redundancy Reduction and Pattern Recognition

Deep, elegant, beautiful? Part of what makes a theory elegant is its power to explain much while assuming little. Here, Darwin's natural selection wins hands down. The ratio of the huge amount that it explains (everything about life: its complexity, diversity and illusion of crafted design) divided by the little that it needs to postulate (non-random survival of randomly varying genes through geological time) is gigantic. Never in the field of human comprehension were so many facts explained by assuming so few. Elegant then, and deep—its depths hidden from everybody until as late as the nineteenth century. On the other hand, for some tastes natural selection is too destructive, too wasteful, too cruel to count as beautiful. In any case, coming late to the party as ever, I can count on somebody else choosing Darwin. I'll take his great grandson instead, and come back to Darwin at the end.

Horace Barlow FRS is the youngest grandchild of Sir Horace Darwin, Charles Darwin's youngest child. Now a very active ninety, Barlow is a member of a distinguished lineage of Cambridge neurobiologists. I want to talk about an idea that he published in two papers in 1961, on redundancy reduction and pattern recognition. It is an idea whose ramifications and significance have inspired me throughout my career.

The folklore of neurobiology includes a mythical 'grandmother neurone', which fires only when a very particular image, the face of Jerry Lettvin's grandmother, falls on the retina (Lettvin was a distinguished American neurobiologist who, like Barlow, worked on the frog retina). The point is that Lettvin's grandmother is only one of countless images that a brain is capable of recognising. If there were a specific neurone for everything we can recognise—not just Lettvin's grandmother but lots of other faces, objects, letters of the alphabet, flowers, each one seen from many angles and distances, we would have a combinatorial explosion. If sensory recognition worked on the 'grandmother principle', the number of specific recognition neurones for all possible combinations of nerve impulses would exceed the number of atoms in the universe. Independently, the American psychologist Fred Attneave had calculated that the volume of the brain would have to be measured in cubic light years. Barlow and Attneave independently proposed redundancy reduction as the answer.

Claude Shannon, inventor of Information Theory, coined 'redundancy' as a kind of inverse of information. In English, 'q' is always followed by 'u', so the 'u' can be omitted without loss of information. It is redundant. Wherever redundancy occurs in a message (which is wherever there is nonrandomness), the message can be more economically recoded without loss of information (although with some loss in capacity to correct errors). Barlow suggested that, at every stage in sensory pathways, there are mechanisms tuned to eliminate massive redundancy.

The world at time t is not greatly different from the world at time t-1. Therefore it is not necessary for sensory systems continuously to report the state of the world. They need only signal changes, leaving the brain to assume that everything not reported remains the same. Sensory adaptation is a well-known feature of sensory systems, which does precisely as Barlow prescribed. If a neurone is signalling temperature, for example, the rate of firing is not, as one might naively suppose, proportional to the temperature. Instead, firing rate increases only when there is a change in temperature. It then dies away to a low resting frequency. The same is true of neurones signalling brightness, loudness, pressure and so on. Sensory adaptation achieves huge economies by exploiting the non-randomness in temporal sequence of states of the world.

What sensory adaptation achieves in the temporal domain, the well-established phenomenon of lateral inhibition does in the spatial domain. If a scene in the world falls on a pixellated screen, such as the back of a digital camera or the retina of an eye, most pixels see the same as their immediate neighbours. The exceptions are those pixels which lie on edges, boundaries. If every retinal cell faithfully reported its light value to the brain, the brain would be bombarded with a massively redundant message. Huge economies can be achieved if most of the impulses reaching the brain come from pixel cells lying along edges in the scene. The brain then assumes uniformity in the spaces between edges.

As Barlow pointed out, this is exactly what lateral inhibition achieves. In the frog retina, for example, every ganglion cell sends signals to the brain, reporting on the light intensity in its particular location on the surface of the retina. But it simultaneously sends inhibitory signals to its immediate neighbours. This means that the only ganglion cells to send strong signals to the brain are those that lie on an edge. Ganglion cells lying in uniform fields of colour (the majority) send few if any impulses to the brain because they, unlike cells on edges, are inhibited by all their neighbours. The spatial redundancy in the signal is eliminated.

The Barlow analysis can be extended to most of what is now known about sensory neurobiology, including Hubel and Wiesel's famous horizontal and vertical line detector neurones in cats (straight lines are redundant, reconstructable from their ends), and in the movement ('bug') detectors in the frog retina, discovered by the same Jerry Lettvin and his colleagues. Movement represents a non-redundant change in the frog's world. But even movement is redundant if it persists in the same direction at the same speed. Sure enough, Lettvin and colleagues discovered a 'strangeness' neurone in their frogs, which fires only when a moving object does something unexpected, such as speeding up, slowing down, or changing direction. The strangeness neurone is tuned to filter out redundancy of a very high order.

Barlow pointed out that a survey of the sensory filters of a given animal could, in theory, give us a read-out of the redundancies present in the animal's world. They would constitute a kind of description of the statistical properties of that world. Which reminds me, I said I'd return to Darwin. In Unweaving the Rainbow, I suggested that the gene pool of a species is a 'Genetic Book of the Dead', a coded description of the ancestral worlds in which the genes of the species have survived through geological time. Natural selection is an averaging computer, detecting redundancies—repeat patterns—in successive worlds (successive through millions of generations) in which the species has survived (averaged over all members of the sexually reproducing species). Could we take what Barlow did for neurones in sensory systems, and do a parallel analysis for genes in naturally selected gene pools? Now that would be deep, elegant and beautiful.

Transitional Objects

I was a student in psychology in the mid-1970s at Harvard University. The grand experiment that had been "Social Relations" at Harvard had just crumbled. Its ambition had been to bring together the social sciences in one department, indeed, most in one building, William James Hall. Clinical psychology, experimental psychology, physical and cultural anthropology, and sociology, all of these would be in close quarters and intense conversation.

But now, everyone was back in their own department, on their own floor. From my point of view, what was most difficult was that the people who studied thinking were on one floor and the people who studied feeling were on another.

In this Balkanized world, I took a course with George Goethals in which we learned about the passion in thought and the logical structure behind passion. Goethals, a psychologist who specialized in adolescence, was teaching a graduate seminar in psychoanalysis. Goethals focus was on a particular school of analytic thought: British object relations theory. This psychoanalytic tradition kept its eye on a deceptively simple question: How do we bring people and what they meant to us "inside" us? How do these internalizations cause us to grow and change? The "objects" of its name were, in fact, people.

Several classes were devoted to the work of David Winnicott and his notion of the transitional object. Winnicott called transitional the objects of childhood—the stuffed animals, the bits of silk from a baby blanket, the favorite pillows—that the child experiences as both part of the self and of external reality. Winnicott writes that such objects mediate between the child's sense of connection to the body of the mother and a growing recognition that he or she is a separate being. The transitional objects of the nursery—all of these are destined to be abandoned. Yet, says Winnicott, they leave traces that will mark the rest of life. Specifically, they influence how easily an individual develops a capacity for joy, aesthetic experience, and creative playfulness. Transitional objects, with their joint allegiance to self and other, demonstrate to the child that objects in the external world can be loved.

Winnicott believes that during all stages of life we continue to search for objects we experience as both within and outside the self. We give up the baby blanket, but we continue to search for the feeling of oneness it provided. We find them in moments of feeling "at one" with the world, what Freud called the "oceanic feeling." We find these moments when we are at one with a piece of art, a vista in nature, a sexual experience.

As a scientific proposition, the theory of the transitional object has its limitations. But as a way of thinking about connection, it provides a powerful tool for thought. Most specifically, it offered me a way to begin to understand the new relationships that people were beginning to form with computers, something I began to study in the late 1970s and early 1980s. From the very beginning, as I began to study the nascent digital culture culture, I could see that computers were not "just tools." They were intimate machines. People experienced them as part of the self, separate but connected to the self.

A novelist using a word processing program referred to "my ESP with the machine. The words float out. I share the screen with my words." An architect who used the computer to design goes went even further: "I don't see the building in my mind until I start to play with shapes and forms on the machine. It comes to life in the space between my eyes and the screen."

After studying programming, a thirteen year old girl said, that when working with the computer, "there's a little piece of your mind and now it's a little piece of the computer's mind and you come to see yourself differently." A programmer talked about his "Vulcan mind meld" with the computer.

When in the late 1970s, I began to study the computer's special evocative power, my time with George Goethals and the small circle of Harvard graduate students immersed in Winnicott came back to me. Computers served as transitional objects. They bring us back to the feelings of being "at one" with the world. Musicians often hear the music in their minds before they play it, experiencing the music from within and without. The computer similarly can be experienced as an object on the border between self and not-self. Just as musical instruments can be extensions of the mind's construction of sound, computers can be extensions of the mind's construction of thought.

This way of thinking about the computer as an evocative objects puts us on the inside of a new inside joke. For when psychoanalysts talked about object relations, they had always been talking about people. From the beginning, people saw computers as "almost-alive" or "sort of alive." With the computer, object relations psychoanalysis can be applied to, well, objects. People feel at one with video games, with lines of computer code, with the avatars they play in virtual worlds, with their smartphones. Classical transitional objects are meant to be abandoned, their power recovered in moments of heightened experience. When our current digital devices—our smartphones and cellphones—take on the power of transitional objects, a new psychology comes into play. These digital objects are never meant to be abandoned. We are meant to become cyborg.

Unconscious Inferences

Optical illusions are a pleasure to look at, puzzling, and robust. Even if you know better, you still are caught in the illusion. Why do they exist? Are they merely mental quirks? The physicist and physiologist Hermann von Helmholtz (182-1894) provided us with a beautiful explanation of the nature of perception, and how it generates perceptual illusions of depth, space, and other properties. Perception requires smart bets called "unconscious inferences."

In Volume III of his Physiological Optics, Helmholtz recalled a childhood experience:

"I can recall when I was a boy going past the garrison chapel in Potsdam, where some people were standing in the belfry. I mistook them for dolls and asked my mother to reach up and get them for me, which I thought she could do. The circumstances were impressed on my memory, because it was by this mistake that I learned to understand the law of foreshortening in perspective."

This childhood experience taught Helmholtz that information available from the retina and other sensory organs is not sufficient to reconstruct the world. Size, distance, and other properties need to be inferred from uncertain cues, which in turn have to be learned by experience. Based on this experience, the brain draws unconscious inferences about what a sensation means. In other words, perception is a kind of bet about what's really out there. But how exactly does this inference work? Helmholtz drew an analogy with probabilistic syllogisms. The major premise is a collection of experiences that are long out of consciousness; the minor premise is the present sensory impression. Consider the "dots illusion" based on V. S.Ramachandran and colleagues.

The dots in the left picture appear concave, receding into the surface away from the observer, while those on the right side appear convex, curved towards the observer. If you turn the page around, the inward dots will pop out and vice versa. In fact, the two pictures are identical, except for being rotated 180 degrees. The illusion of concave and convex dots occurs because our brain makes unconscious inferences.

Major premise: A shade on the upper part of a dot is nearly always associated with a concave shape.
Minor premise: The shade is in the upper part
Unconscious inference: The shape of the dot is concave.

Our brains assumes a three-dimensional world, and the major premise guesses the third dimension from two ecological structures:

1. Light comes from above, and 
2. There is only one source of light.

These two structures dominated most of human and mammalian history, in which the sun and the moon were the only sources of light, and the first also holds approximately for artificial light today. Helmholtz would have favored the view that the major premise is learned from individual experience, others have favored evolutionary learning. In both cases, visual illusions are seen as the product of unconscious inferences based on evidence that is usually reliable, but can be fooled in special circumstances.

The concept of unconscious inference can also explain phenomena from other sensory modalities. A remarkable instance where a major premise suddenly becomes incorrect is the case of a person whose leg has been amputated. Although the major premise ("A stimulation of certain nerves is associated with that toe") no longer holds, patients nevertheless feel pain in toes that are no longer there. The "phantom limb" also illustrates our inability to correct unconscious inferences in spite of better knowledge. Helmholtz's concept of unconscious inferences has given us a new perspective on perception in particular and cognition in general.]

1.Cognition is inductive inference. Today, the probabilistic syllogism has been replaced by statistical and heuristic models of inference, inspired by Thomas Bayes and Herbert Simon, respectively. 
2.Rational inferences need not be conscious. Gut feelings and intuition work with the same inductive inferences as conscious intelligence. 
3.Illusions are a necessary consequence of intelligence. 

Cognition requires going beyond the information given, to make bets and therefore to risk errors. Would we better off without visual illusions? We would in fact be worse off—like a person who never says anything to avoid making any mistakes. A system that makes no errors is not intelligent. 

The Power Of One, Two, Three

Sometimes even the simple act of counting can tell you something profound.

One day, back in the late 1990s, when I was a correspondent for New Scientist magazine, I got an e-mail from a flack waxing rhapsodic about an extraordinary piece of software. It was a revolutionary data-compression program so efficient that it would squash every digital file by 95% or more without losing a single bit of data. Wouldn't my magazine jump at the chance to tell the world about the computer program that will make their hard drives hold 20 times more information than every before.

No, my magazine wouldn't.

No such compression algorithm could possibly exist; it was the algorithmic equivalent of a perpetual motion machine. The software was a fraud.

The reason: the pigeonhole principle.

The pigeonhole principle is a simple counting argument. It says that if you've got N pigeons and manage to stuff them into fewer than N boxes, then at least one box must have more than one pigeon in it. As blindingly obvious as this is, it's a powerful tool.

For example, imagine that the compression software really worked as advertised, and every file is shrunk by a factor of 20 without any loss of fidelity. Every single file 2000 bits long will be squashed down into a mere 100 bits, and then, when the algorithm is reversed, it expands back into its original form, unscathed.

When compressing files, you bump up against the pigeonhole principle. There are many more 2000-bit pigeons (2²⁰⁰⁰, to be exact) than 100-bit boxes (2¹⁰⁰). If an algorithm stuffs the former into the latter, at least one box must contain multiple pigeons. Take that box
—that 100-bit file—and reverse the algorithm, expanding the file into its original 2000-bit form. You can't! Since there are multiple 2000-bit files which all wind up being squashed into to the same 100-bit file, the algorithm has no way of knowing which one was the true original—it can't reverse the compression.

The pigeonhole principle puts an absolute limit on what a compression algorithm can do. It can compress some files—often dramatically—but it can't compress them all, at least if you insist on perfect fidelity.

Counting arguments similar to this one have opened up entire new realms for us to explore. Georg Cantor used a kind of reverse-pigeonhole-principle technique to show that it was impossible to fit the real numbers into boxes labeled by the integers—even though there are an infinite number of integers. The almost unthinkable consequence was that there were different levels of infinity; the infinity of the integers was dwarfed by the infinity of the reals, which, in turn is dwarfed by yet another infinity and another infinity on top of that... an infinity of infinities, all unexplored until we learned to count them.

Taking the pigeonhole principle into deep space has an even stranger consequence. A principle in physics, the holographic bound, implies that in any finite volume of space, there are only a finite number of possible configurations of matter and energy in that space. If, as cosmologists tend to believe, the universe is infinite, there are an infinite number of visible-universe-sized volumes out there—enormous cosmos-sized bubbles containing matter and energy. And if space is more or less homogeneous, there's nothing particularly special about the cosmos-sized-bubble we live in. These assumptions, taken together, lead to a stunning conclusion. Infinite universe-sized bubbles, with only a finite number of configurations of the matter and energy in those bubbles mean that there's not just an exact copy of our universe—and our earth—out there, the transfinite version of the pigeonhole principle states that there's an infinite number of copies of every (technically, "almost every," which has a precise mathematical definition) possible universe. Not only are there infinite copies of you on infinite alternate Earths, there are infinite copies of countless variations upon the theme: versions of you with a prehensile tail, versions of you with multiple heads, versions of you that have made a career juggling carnivorous rabbit-like animals in exchange for costume jewelry.

Even something as simple as counting one, two, three can lead to a completely unexpected realm.

The Beautiful Law of Unintended Consequences

According to the guide on my walking tour of The Rocks neighborhood in Sydney, Australia, when the plague hit the city around 1900, a bounty was placed on rats to encourage people to kill them, since it was known that rats bore the fleas that communicated the disease to humans. The intent of the bounty was plain enough: reducing the number of rats to reduce the spread of the plague. An unintended consequence, however, was that residents, tempted by the rat bounty, began breeding rats.

The law of unintended consequences is often associated with Robert Merton, though its general spirit appears in various forms, not least in Adam Smith’s invisible hand notion, and is somehow delightful in its chaos, as if Nature continually thumbs her nose at our attempts to control her.

The idea is that when people intervene in systems with a lot of moving parts, especially ecologies and economies, because of the complex interrelationships among parts of the system, the intervention will have effects beyond those that were intended, including many that were unforeseen or unforeseeable.

Examples abound. Returning to Australia, one of the best known examples of an unintended consequence is the case of rabbits, brought by the First Fleet as food, released into the wild for hunting, with the unintended consequence that rabbit populations grew to staggering proportions, causing untold ecological devastation, in turn leading to the development of measures to control the rabbits, including an exceptionally long fence, which had the unintended consequence of guiding three young girls home in the 1930s, which in turn had the unintended consequence of inspiring an award-winning motion picture (Rabbit Proof Fence) with a soundtrack by Peter Gabriel.

These chains of consequences occur because making changes to one part of a system with many interacting parts leads to changes in other parts of the system. Because many of the systems that we try to influence are complex but incompletely understood—bodies, habitats, markets—there are bound to be consequences that are difficult to predict.

This is not to say that the consequences will always be undesirable. Recently, certain municipalities changed the laws governing the use of marijuana, making it easier to obtain for medical purposes. The law might or might not have reduced the suffering of glaucoma victims, but data from traffic accidents suggest that the change in the legislation did reduce fatalities on the road by about 9%. (People substituted marijuana for alcohol and apparently drive better stoned than drunk.) Saving drivers’ lives was not the intent of the law, but that was the effect.

Another example, smaller in scale though closer to my heart, was the recent abrupt increase of parking rates by a third in University City, Philadelphia, where I work. The intent of the law was to raise revenue to help fund the city’s schools. An unintended consequence—because students seem disinclined to pay the higher price—is that I can rely on getting a parking spot when I have to drive to school.

Intervention in any sufficiently complicated system is bound to produce unintended effects. We treat patients with antibiotics, and we select for resistant strains of pathogens. We artificially select for wrinkly-faced bulldogs, and less pleasant traits, such as respiratory problems, come along for the ride. We treat morning sickness with thalidomide, and babies with birth defects follow.

In the economic sphere, most policies have various sorts of knock on effects, with prohibitions and bans providing some of the most profound examples, including, of course, Prohibition in America, which spun off various consequences including, arguably, the rise of organized crime in the United States. Because governments typically only ban things for which people have a taste, when bans do arise, people find ways to satisfy these tastes, either through substitutes or black markets, both of which lead to varied consequences. Ban sodas, give a boost to sports drink sales. Ban the sale of kidneys, spawn an international black market for organs and underground surgeries. Ban hunting mountain lions, endanger local joggers. (Not because joggers are substituted for mountain lions as prey for hunters; the ban increased the mountain lion population, who in turn menaced joggers.)

There is something oddly beautiful about the tendrils of causality in complex systems, holding the same appeal that we find in the deliberate inelegance of Rube-Goldberg machines. And none of this is to say that the inevitable possibilities of being surprised by our interventions means that we must give in to pessimism. Rather, it is a reminder to have caution and humility. As we gradually increase our understanding of large, complicated systems, we will develop new ways to glimpse the unintended consequences of our actions. We already have some guiderails—people will substitute for banned or taxed products; removing one species in an ecology typically penalizes populations that prey on them and aids species that compete with them, and so on—so while there will probably be always unintended consequences, these consequences won’t always be completely unanticipated. 

Developmental Timing Explains The Woes Of Adolescence

"What was he thinking!" This is the familiar bewildered cry of parents trying to explain why their teenaged children act the way they do. Developmental psychologists, neuroscientists and clinicians have an interesting and elegant explanation for teenage weirdness. It applies to a wide range of adolescent behavior, from the surprisingly admirable, to the mildly annoying, to the downright pathological. The idea is that there are two different neural and functional systems that interact to turn children into adults. The developmental relationship between those two systems has changed, and that, in turn, has profoundly changed adolescence.

First, there is a motivational and emotional system that is very closely linked to the biological and chemical changes of puberty. This is what turns placid ten-year-olds, safe in the protected immaturity of childhood, into restless, exuberant, emotionally intense teenagers, desperate to attain every goal, fulfill every desire, and experience every sensation. And for adolescents, the most important goal of all is to get the respect of your peers. Recent studies show that adolescents aren't reckless because they underestimate risks, but because they overestimate rewards, especially social rewards, or rather that they find rewards more rewarding than adults do—think about the incomparable intensity of first love, the never to be recaptured glory of the high-school basketball championship. (In youth you want things, and then in middle-age you want to want them.)

The second system is a control system that can channel and harness all that seething energy. The prefrontal cortex reaches out to guide and control other parts of the brain. This is the system that inhibits impulses and guides decision-making. This control system depends much more on learning than the motivational system. You get to make better decisions by making not so good decisions and then correcting them. You get to be a good planner by making plans, implementing them and seeing the results again and again. Expertise comes with experience.

In the distant evolutionary past, in fact, even in the recent historical past, these two systems were in sync. Most childhood education involved formal and informal apprenticeships. Children had lots of chances to practice exactly the skills that they would need to accomplish their goals as adults, and so to become expert planners and actors. To become a good gatherer or hunter, cook or caregiver, you would actually practice gathering, hunting, cooking and taking care of children all through middle-childhood and early adolescence—tuning up just the prefrontal wiring you'd need as an adult. But you'd do all that under expert adult supervision and in the protected world of childhood where the impact of your inevitable failures would be blunted. When the motivational juice of puberty kicked in, you'd be ready to go after the real rewards with new intensity and exuberance, but you'd also have the skill and control to do it effectively and reasonably safely.

In contemporary life though, the relationship between these two systems has changed. For reasons that are somewhat mysterious but most likely biological, puberty is kicking in at an earlier and earlier age. (The leading theory points to changes in energy balance as children eat more and move less). The motivational system kicks in with it.

At the same time, contemporary children have very little experience with the kinds of tasks that they'll have to perform as grown-ups. Children have increasingly little chance to even practice such basic skills as cooking and caregiving. In fact, contemporary adolescents and preadolescents often don't do much of anything except go to school. The experience of trying to achieve a real goal in real time in the real world is increasingly delayed, and the development of the control system depends on just those experiences. The developmental psychologist Ron Dahl has a nice metaphor for the result—the adolescents develop a gas pedal and accelerator a long time before they get steering and brakes.

This doesn't mean that adolescents are stupider than they used to be — in many ways, they are much smarter. In fact, there's even some evidence that delayed frontal development is correlated with higher I.Q. The increasing emphasis on schooling means that children know more about more different subjects than they ever did in the days of apprenticeships. Becoming a really expert cook doesn't tell you about the evolution of tool-use or the composition of sodium chloride—the sorts of things you learn in school. But there are different ways of being smart-knowing history and chemistry is no help with a soufflé. Wide-ranging, flexible and broad-based learning may actually be in tension with the ability to develop finely-honed controlled, focused expertise in a particular skill.

Of course, the old have always complained about the young. But the explanation does elegantly account for the paradoxes and problems of our particular crop of adolescents. There do seem to be many young adults who are enormously smart and knowledgeable but directionless, who are enthusiastic and exuberant but unable to commit to a particular work or a particular love until well into their twenties or thirties. And there is the graver case of children who are faced with the uncompromising reality of the drive for sex, power and respect, without the expertise and impulse-control it takes to ward off pregnancy or violence.

I like this explanation because it accounts for so many puzzling everyday phenomena. But I also like it because it emphasizes two really important facts about minds and brains that are often overlooked. First, there's the fact that experience shapes the brain. Its truer to say that our experience of controlling our impulses make the prefrontal cortex develop than it is to say that prefrontal development makes us better at controlling our impulses.

Second, it's increasingly apparent that development plays a crucial role in explaining human nature. The old "evolutionary psychology" picture was that a small set of genes was directly responsible for some particular pattern of adult behavior—a "module". In fact, there is more and more evidence that genes are just the first step in complex developmental sequences, cascades of interactions between organism and environment, and that those developmental processes shape the adult brain. Even small changes in developmental timing can lead to big changes in who we become.

The Elementary Particles of Memory

The most complicated structure in the universe known to us is the human brain, composed of 100 billion neurons. There are two aspects of this complexity. First is the circuit plan of our brains, encoded by the sequence of A, C, G, and T's in DNA, together with its epigenetic changes. This circuitry is our behavioral inheritance as Homo sapiens, endowing us with "vegetative" functions, like sleeping and eating, a basic cognitive toolbox, including perhaps the basics of grammar and counting, and individual tendencies, such as resilience or susceptibility to stress.

But the information encoding this complicated circuitry is miniscule compared with the range and capacity of human thought. An individual thought is due to the firing of a specific population of neurons, which is determined by ongoing sensory input in the present, and the ensembles of neurons within the basic circuitry that have been linked together by experiences in the past — our memories. This linkage, the physical basis of memory, is due to the experience-dependent, persistent strengthening or weakening of synapses, which allow specific groups of neurons to more easily fire together, even if only a few of the neurons in the group are activated by a sensory input. Each neuron has ~10,000 synaptic connections with other neurons. Thus the patterns created by the potential strengthening and weakening of a quadrillion synapses determine the number of potential memories in an individual.

Underlying this complexity, however, is a simple and deep organization to the changes in synaptic strength that keep these populations of neurons together to sustain long-term memories— a handful of physiological processes maintained by a few essential molecules. The first of these physiological processes, called long-term potentiation (LTP), was discovered in 1966 by Terje Lømo, who worked with Tim Bliss to produce the first systematic study of LTP in 1973. LTP is a persistent strengthening of synaptic connections triggered by a brief episode of high-frequency activity of those connections. The second physiological mechanism to store long-term information was discovered by Gary Lynch and Tom Dunwiddie in 1978, and is the inverse of LTP, long-term depression (LTD), a persistent weakening of synapses that is triggered by a different pattern of activity.

There are hundreds of molecules in the synapse that regulate the formation of LTP, but only a few that maintain the persistent strengthening over time. The key molecule maintaining LTP is a persistently active enzyme, called PKMzeta. Together with the molecules maintaining LTD that are still being determined, these elementary molecules store most forms of memory. Without the persistent strengthening of synapses by PKMzeta, the ongoing physiological process of LTP at the synapse collapses, and most long-term memories are erased. The animal returns to a "blank slate," with just its genetic inheritance of behavior.

The molecular mechanism for the formation of PKMzeta likely evolved over 500 million years ago in the Cambrian period. This event was a mutation in a gene critical for the development of polarized structures in cells, such as the wall of an epithelial cell that faces the inside of the gut, or a synapse of a neuron. The gene is for a protein kinase, an enzyme that catalyzes chemical reactions. But PKMzeta is an unusual form of protein kinase. Once made when LTP is triggered, PKMzeta is active all the time, rather than being turned on and off in response to other molecules. When mutations occur in genes for kinases that render them active all the time, they promote uncontrolled growth in cells, leading to cancer. However, the change in the gene that encodes PKMzeta also restricts the formation of the persistently active kinase to neurons. Because mature neurons are tethered to thousands of other neurons through their synapses, they cannot possibly divide and are remarkably resistant to forming cancers (most brain tumors in adults originate from glial cells, which readily divide). By restriction to cells that communicate but cannot divide, a mutation signaling continual growth, potentially deadly to an organism, was used to maintain long-term memory.

Without this accident in the Cambrian, life would have continued, the nervous systems of vertebrates would have evolved, and the behaviors of animals might have become quite complex, but no information could have been stored other than the slow accretion of instinct by natural selection. There would be no record of an animal's experience within its life, and for humans no culture, no knowledge of the world. For an individual, a consciousness that reflects on the narrative of one's life would be inconceivable.

Nature is More Clever Than We Are

We have the clear impression that our deliberative mind makes the most important decisions in our life: What work we do, where we live, who we marry. But contrary to this belief the biological evidence points toward a decision process in an ancient brain system called the basal ganglia, brain circuits that consciousness cannot access. Nonetheless, the mind dutifully makes up plausible explanations for the decisions.

The scientific trail that led to this conclusion began with honeybees. Worker bees forage the spring fields for nectar, which they identify with the color, fragrance and shape of a flower. The learning circuit in the bee brain converges on VUMmx1, a single neuron that receives the sensory input and, a bit later, the value of the nectar, and learns to predict the nectar value of that flower the next time the bee encounters it. The delay is important because the key is prediction, rather than a simple association. This is also the central core of temporal-difference (TD) learning, which can learn a sequence of decisions leading to a goal and is particularly effective in uncertain environments like the world we live in.

Buried deep in your midbrain there is a small collection of neurons, found in our earliest vertebrate ancestors, that project throughout the cortical mantle and basal ganglia that are important for decision making. These neurons release a neurotransmitter called dopamine, which has a powerful influence on our behavior. Dopamine has been called a "reward" molecule, but more important than reward itself is the ability of these neurons to predict reward: If I had that job, how happy would I be? Dopamine neurons, which are central to motivation, implement TD learning, just like VUMmx1.

TD learning solves the problem of finding the shortest path to a goal. It is an "online" algorithm because it learns by exploring and discovers the value of intermediate decisions in reaching the goal. It does this by creating an internal value function, which can be used to predict the consequences of actions. Dopamine neurons evaluate the current state of the entire cortex and inform the brain about the best course of action from the current state. In many cases the best course of action is a guess, but because guesses can be improved, over time TD learning creates a value function of oracular powers. Dopamine may be the source of the "gut feeling" you sometime experience, the stuff that intuition is made from.

When you consider various options, prospective brain circuits evaluate each scenario and the transient level of dopamine registers the predicted value of each decision. The level of dopamine is also related to your level of motivation, so not only will a high level of dopamine indicate a high expected reward, but you will also have a higher level of motivation to pursue it. This is quite literally the case in the motor system, where a higher tonic dopamine level produces faster movements. The addictive power of cocaine and amphetamines is a consequence of increased dopamine activity, hijacking the brain's internal motivation system. Reduced levels of dopamine lead to anhedonia, an inability to experience pleasure, and the loss of dopamine neurons results in Parkinson's Disease, an inability to initiate actions and thoughts.

TD learning is powerful because it combines information about value along many different dimensions, in effect comparing apples and oranges in achieving distant goals. This is important because rational decision-making is very difficult when there many variables and unknowns, so having an internal system that quickly delivers good guesses is a great advantage, and may make the difference between life and death when a quick decision is needed. TD learning depends on the sum of your life experiences. It extracts what is essential from these experiences long after the details of the individual experiences are no longer remembered.

TD learning also explains many of the experiments that were performed by psychologists who trained rats and pigeons on simple tasks. Reinforcement learning algorithms have traditionally been considered too weak to explain more complex behaviors because the feedback from the environment is sparse and minimal. Nonetheless reinforcement learning is universal among nearly all species and is responsible for some of the most complex forms of sensorimotor coordination, such as piano playing and speech. Reinforcement learning has been honed by hundreds of millions of years of evolution. It has served countless species well, in particular our own.

How complex a problem can TD learning solve? TD gammon is a computer program that learned how to play backgammon by playing itself. The difficulty with this approach is that the reward comes only at the end of the game, so it is not clear which were the good moves that led to the win. TD gammon started out with no knowledge of the game, except for the rules. By playing itself many times and applying TD learning to create a value function to evaluation game positions, TD gammon climbed from beginner to expert level, along the way picking up subtle strategies similar to ones that humans use. After playing itself a million times it reached championship level and was discovering new positional play that astonished human experts. Similar approaches to the game of Go have achieved impressive levels of performance and are on track to reach professional levels.

When there is a combinatorial explosion of possible outcomes, selective pruning is helpful. Attention and working memory allow us to focus on most the important parts of a problem. Reinforcement learning is also supercharged by our declarative memory system, which tracks unique objects and events. When large brains evolved in primates, the increased memory capacity greatly enhanced the ability to make more complex decisions, leading to longer sequences of actions to achieve goals. We are the only species to create an educational system and to consign ourselves to years of instruction and tests. Delayed gratification can extend into the distant future, in some cases extending into an imagined afterlife, a tribute to the power of dopamine to control behavior.

At the beginning of the cognitive revolution in the 1960s the brightest minds could not imagine that reinforcement learning could underlie intelligent behavior. Minds are not reliable. Nature is more clever than we are.

The Discontinuity of Science and Culture

From time to time, large sections of humanity find themselves, at short notice, in a different universe. Science, culture and society have undergone a tectonic shift, for better or worse—the rise of a powerful religious or political leader, the Declaration of Independence, the end of slavery—or, on the other hand, the fall of Rome, the Great Plague, the World Wars.

So, too in the world of art. Thus, Virginia Woolf said famously, "In or about December 1910, human character changed", owing, in her view, to the explosive exhibition of post-impressionist canvases in London that year. And after the discovery of the nucleus was announced, Wassily Kandinsky wrote: "The collapse of the atom model was equivalent, in my soul, to the collapse of the whole world. Suddenly, the thickest walls fell...", and he could turn to a new way of painting.

Each of such world-view changing occurrences tend to be deeply puzzling or anguishing. They are sudden fissures in the familiar fabric of history that ask for explanations, with treatises published year after year, each hoping to provide an answer, seeking the cause of the dismay.

I will here focus on one such phenomenon.

In 1611, John Donne published his poem, "The First Anniversary", containing the familiar lines "And new Philosophy has all in doubt,/ the Element of fire is quite put out..." and later, " ...Is crumbled out againe to his Atomies/ 'Tis all in peeces, all cohaerence gone/ All just supply and all Relation." He and many others felt the old order and unity had been displaced by relativism and discontinuity.

The explanation for his anguish was as an entirely unexpected event the year before: Galileo's discovery of the fact that the moon has mountains, that Jupiter has moons, that there are immensely more stars than had been known.

Of this happening and its consequent findings, the historian Marie Nicolson wrote: "We may perhaps date the beginning of modern thought from the night of January 7, 1610 when Galileo, by means of the instrument he developed [the telescope], thought he perceived new planets and new, expanded worlds."

Indeed, by his work Galileo gave a deep and elegant explanation for the question how our cosmos is arranged—no matter how painful this may have been to the Aristotelians and poets of his time. At last, the Copernican theory, formulated long ago, had more credibility. From this vast step forward, new science and new culture could be born.

Moore's Law

Moore's Law originated in a four page 1965 magazine article written by Gordon Moore, then at Fairchild Semiconductor and later one of the founders of Intel. In it he predicted that the number of components on a single integrated circuit would rise from the then current number of roughly two to the sixth power, to roughly two to the sixteenth power in the following ten years, i.e., the number of components would double every year. He based this on four empirical data points and one null data point, fitting a straight line on a graph plotting the log of the number of components on a single chip against a linear scale of calendar years. Intel later amended Moore's Law to say that the "number of transistors on a chip roughly doubles every two years".

Moore's law is rightly seen as the fundamental driver of the information technology revolution in our world over the last fifty years as doubling the number of transistors every so often has made our computers twice as powerful for the same price, doubled the amount of data they can store or display, made them twice as fast, made them smaller, made them cheaper and in general improved them in every possible way by a factor of two on a clockwork schedule.

But why does it happen? Automobiles have not obeyed Moore's Law, neither have batteries, nor clothing, nor food production, nor the level of political discourse. All but the last have demonstrably improved due to the influence of Moore's Law, but none have had the same relentless exponential improvements.

The most elegant explanation for what makes Moore's Law possible is that digital logic is all about an abstraction, and in fact a one-bit abstraction, a yes/no answer to a question, and that abstraction is independent of physical bulk.

In a world that consists entirely of piles of red sand and piles of green sand, the size of the piles is irrelevant. A pile is either red or green, and you can take away half the pile, and it is still either a pile of red sand or a pile of green sand. And you can take away another half, and another half, and so on, and still the abstraction is maintained. And repeated halving at a constant rate makes an exponential.

That is why Moore's Law works on digital technology, and doesn't work on technologies that require physical strength, or physical bulk, or must deliver certain amounts of energy. Digital technology uses physics to maintain an abstraction and nothing more.

Some caveats do apply:

1. In his short paper Moore expressed some doubt as to whether his prediction would hold for linear, rather than digital, integrated circuits as he pointed out that by their nature, "such elements require the storage of energy in a volume" and that the volume would necessarily be large.

2. It does matter when you get down to piles of sand with just one grain, and then technology has to shift and you need to use some new physical property to define the abstraction—such technology shifts have happened again and again, in the maintenance of Moore's Law over almost fifty years.

3. It does not explain the sociology of how Moore's Law is implemented and what determines the time constant of a doubling, but it does explain why exponentials are possible in this domain. 

Simplicity

We all have an intuitive sense of what "simplicity" means. In science, the word is often used as a term of praise. We expect that simple explanations are more natural, sounder, and more reliable than complicated ones. We abhor epicycles, or long lists of exceptions and special cases.

But can we take a crucial step further, to refine our intuitions about simplicity into precise, scientific concepts? Is there a simple core to "simplicity"? Is simplicity something we can quantify, and measure?

When I think about big philosophical questions, which I probably do more than is good for me, one of my favorite techniques is to try to frame the question in terms that could make sense to a computer. Usually it's a method of destruction: It forces you to be clear, and once you dissipate the fog you discover that very little of your big philosophical question remains. Here, however, in coming to grips with the nature of simplicity, the technique proved creative, for it led me straight toward a (simple) profound idea in the mathematical theory of information, the idea of description length. (The idea goes by several different names in the scientific literature, including algorithmic entropy and Kolmogorov-Smirnov-Chaitin complexity. Naturally, I chose the simplest one.)

Description length is actually a measure of complexity, but for our purposes that's just as good, since we can define simplicity as the opposite—or, numerically, the negative—of complexity. To ask a computer how complex something is, we have to present that "something" in a form the computer can deal with, that is as a data file, i.e. a string of 0s and 1s. That's hardly a crippling constraint: We know that data files can represent movies, for example, so we can ask how about the simplicity of anything we can present in a movie; since our movie might be a movie recording scientific observations or experiments, we can ask about the simplicity of a scientific explanation.

Interesting data files might be very big, of course. But big files need not be genuinely complex; for example, a file containing trillions of 0s and nothing else isn't genuinely complex. The idea of description length is, simply, that a file is only as complicated as its simplest description. Or, to put it in terms a computer could relate to: A file is as complicated as the shortest program that can produce it from scratch. This defines a precise, widely applicable, numerical measure of simplicity.

An impressive virtue of this notion of simplicity is that illumines and connects up other attractive, successful ideas. Consider, for example, the method of theoretical physics. In theoretical physics, we try to summarize the results of a vast number of observations and experiments in terms of a few powerful laws. We strive, in other words, to produce the shortest possible program that outputs the world. In that precise sense, it's a quest for simplicity.

It's appropriate to add that symmetry, a central feature of the physicist's laws, is a powerful simplicity enabler. For example, if we work with laws that have symmetry under space and time translation—in other words, laws that apply uniformly, everywhere and everywhen—then we don't need to spell out new laws for distant parts of the universe or for different historical epochs, and we can keep our world-program short.

Simplicity leads to depth: For a short program to unfold into rich consequences, it must support long chains of logic and calculation, which are the essence of depth.

Simplicity leads to elegance: The shortest programs will contain nothing gratuitous. Every bit will play a role, for otherwise we could expunge it, and make the program shorter. And the different parts will have to function together smoothly, in order to make a lot from a little. Few processes are more elegant, I think, than the construction, following the program of DNA, of a baby from a fertilized egg.

Simplicity leads to beauty: For it leads, as we've seen, to symmetry, which is an aspect of beauty. As, for that matter, are depth and elegance.

Thus simplicity, properly understood, explains what it is that makes a good explanation deep, elegant, and beautiful.

Time Perspective Theory

I am here to tell you that the most powerful influence on our every decision that can lead to significant action outcomes is something that most of us are both totally unaware of and at the same time is the most obvious psychological concept imaginable.

I am talking about our sense of psychological time, more specifically, the way our decisions are framed by the time zones that you have learned to prefer and tend to overuse. We all live in multiple time zones, learned from childhood, shaped by education, culture, social class, and experiences with economic and family stability-instability. For most of us, we develop a biased temporal orientation that favors one time frame over others, becoming excessively oriented to past, present, or the future.

Thus, at decision time for major or minor judgments, some of us are totally influenced by factors in the immediate situation: The stimulus qualities, what others are doing, saying, urging, and one’s biological urges. Others facing the same decision matrix ignore all those present qualities by focusing instead on the past, the similarities between current and prior settings, remembering what was done and its effects. Finally, a third set of decision makers ignores the present and the past by focusing primarily on the future consequences of current actions, calculating costs vs. gains.

To complicate matters, there are sub domains of each of these primary time zones. Some past-oriented people tend to focus on negatives in their earlier experiences, regret, failure, abuse, trauma, while others are primarily past positive, focusing instead on the good old days, nostalgia, gratitude, and successes. There are two ways to be present-oriented, to live in present- hedonistic domain of seeking pleasure and novelty, and sensation seeking versus being present- fatalistic, living in a default present by believing nothing one does can make any changes in one’s future life. Future-oriented people are goal setters, plan strategies, tend to be successful, but another future focus is on the transcendental future—life begins after the death of the mortal body.

My interest in Time Perspective Theory inspired me to create an inventory to make it possible to determine exactly the extent to which we fit into each of these six time zones. The Zimbardo Time Perspective Inventory, or ZTPI correlates scores on these time dimensions with a host of other psychological traits and behaviors. We have demonstrated that Time Perspective has a major impact across a vast domain of human nature. In fact, some of the relationships uncovered reveal correlation coefficients much greater than ever seen in traditional personality assessment. For example, Future orientation correlates .70 with the trait of conscientiousness, which in turn predicts to longevity. Present Hedonism correlates .70 with sensation seeking and novelty seeking. Those high on Past Negative are most likely to be high on measures of anxiety, depression and anger, with correlations as robust as .75. Similarly substantial correlations are uncovered between Present Fatalism and these measures of personal distress. I should add that this confirmatory factor analysis was conducted on a sample of functioning college students, thus such effects should be cause for alarm by counselors. Beyond mere correlations of scale measures, the ZTPI scales predict to a wide range of behaviors: Course grades, risk taking, alcohol, drug use and abuse, environmental conservation, medical checkups, creativity, problem solving, and much more.  

Finally, one of the most surprising discoveries is the application of Time Perspective theory to time therapy in “curing” PTSD in Veterans, as well as in sexually abused women or civilians suffering from motor vehicle fatality experiences. Dr. Richard Sword and Rosemary Sword have been treating with remarkably positive outcomes a number of veterans from all US recent wars and also civilian clients. The core of the treatment replaces the Past Negative and Present Fatalistic biased time zones common to those suffering from PTSD with a balanced time perspective that highlights the critical role of the hope-filled future, adds in some selected present hedonism, and introduces memories of a Past Positive nature. In a sample of 30 PTSD vets of varying ages and ethnicities, treated with Time Perspective Therapy for a relatively few sessions (compared to traditional cognitive behavioral therapies), dramatic positive changes have been found for all PTSD standard assessments, as well as in life-changing social and professional relationships.  It is so rewarding to see many of our honored veterans who have continued to suffer for decades from their combat-related severe traumas to discover a new life rich with opportunities, friends, family, fun and work by being exposed to this simple, elegant reframing of their mental orientation toward the life of their time.

Metaphors are in the mind

Group Polarization

Forty-five years ago, some social psychological experiments posed story problems that assessed people's willingness to take risks (for example, what odds of success should a budding writer have in order to forego her sure income and attempt writing a significant novel?). To everyone's amazement, group discussions in various countries led people to advise more risk, setting off a wave of speculation about group risk taking by juries, business boards, and the military.

Alas, some other story problems surfaced for which group deliberation increased caution (should a young married parent with two children gamble his savings on a hot stock tip?).

Out of this befuddlement—does group interaction increase risk, or caution?—there emerged a deeper principle of simple elegance: group interaction tends to amplify people's initial inclinations (as when advising risk to the novelist, and caution in the investing).

This "group polarization" phenomenon was then repeatedly confirmed. In one study, relatively prejudiced and unprejudiced students were grouped separately and asked to respond—before and after discussion—to racial dilemmas, such as a conflict over property rights versus open housing. Discussion with like-minded peers increased the attitude gap between the high- and low-prejudiced groups.

Fast forward to today. Self-segregation with kindred spirits is now rife. With increased mobility, conservative communities attract conservatives and progressive communities attract progressives. As Bill Bishop has documented, the percentage of landslide counties—those voting 60 percent or more for one presidential candidate—nearly doubled between 1976 and 2008. And when neighborhoods become political echo chambers, the consequence is increased polarization, as David Schkade and colleagues demonstrated by assembling small groups of Coloradoans in liberal Boulder and conservative Colorado Springs. The community discussions of climate change, affirmative action, and same-sex unions further diverged Boulder folks leftward and Colorado Springs folks rightward.

Terrorism is group polarization writ large. Virtually never does it erupt suddenly as a solo personal act. Rather, terrorist impulses arise among people whose shared grievances bring them together. In isolation from moderating influences, group interaction becomes a social amplifier.

The Internet accelerates opportunities for like-minded peacemakers and neo-Nazis, geeks and goths, conspiracy schemers and cancer survivors, to find and influence one another. When socially networked, birds of a feather find their shared interests, attitudes, and suspicions magnified.

Ergo, one elegant and socially significant explanation of diverse observations is simply this: opinion segregation + conversation → polarization. 

How the Leopard Got His Spots

In one of his celebrated just-so stories, Rudyard Kipling recounted how the leopard got his spots. But taking this approach to its logical conclusion, we would need distinct stories for every animal's pattern: the leopard's spots, the cow's splotches, the panther's solid colors. And we would have to add even more stories for the complex patterning of everything from molluscs to tropical fish.

But far from these different animals requiring separate and distinct explanations, there is a single underlying explanation that shows how we can get all of these varied and different patterns using a single unified theory.

Beginning in 1952, with Alan Turing's publication of a paper entitled "The Chemical Basis of Morphogenesis", scientists recognized a simple set of mathematical formulas could dictate the variety of how patterns and colorings form in animals. This model is known as a reaction-diffusion model and works in a simple way: imagine you have multiple chemicals, which diffuse over a surface at different rates and can interact. While in most cases, diffusion simply creates a uniformity of a given chemical—think how pouring cream into coffee will eventually spread and dissolve and create a lighter brown—when multiple chemicals diffuse and interact, this can give rise to non-uniformity. Even though this sounds somewhat counterintuitive, not only can it occur, but it can be generated using only a simple set of equations, and in turn explain the exquisite variety of patterns seen in the animal world.

Mathematical biologists have been exploring the properties of reaction-diffusion equations ever since Turing's paper. They've found that varying the parameters can generate the animal patterns we see. Some mathematicians have even examined the ways in which the size and shape of the surface can dictate the patterns that we see. As the size parameter is modified, we can easily go from such patterns as giraffe-like to those seen on Holstein cows.

This elegant model can even yield simple predictions. For example, while a spotted animal can have a striped tail (and very often does) according to the model, a striped animal will never have a spotted tail. And this is exactly what we see! These equations can generate the endless variation seen in Nature, but can also show the limitations inherent in biology. The just-so of Kipling may be safely exchanged for the elegance and generality of reaction-diffusion equations.

Seeing Is Believing: From Placebos To Movies In Our Brain

Our brain of one hundred billion neurons and a quadrillion of synapses, give or take a few billion here or there, has to be considered one of the most complex entities to demystify. And that may be a good thing, since we don't necessarily want others to be able to read our minds, which would not only be regarded as terribly invasive, but also taking the recent megatrend of transparency much too far.

But the ability to use functional magnetic resonance (fMRI) and positron emission tomography (PET) to image the brain and construct sophisticated activation maps is fulfilling the "seeing is believing" aphorism for any skeptics. One of the longest controversies in medicine has been whether the placebo effect, a notoriously complex, mind-body end product, has a genuine biological mechanism. That now seems to be resolved with the recognition that the opiod drug pathway — the one that is induced by drugs like morphine and oxycontin—shares the same brain activation pattern as seen with the administration of placebo for pain relief. And just like we have seen neuroimaging evidence of dopamine "squirts" from our Web-based networking and social media engagement, dopamine release from specific regions of the brain has been directly visualized after administering a placebo to patients with Parkinson's disease. Indeed, the upgrading of the placebo effect to having discrete, distinguishable psychobiological mechanisms has now even evoked the notion of deliberately administering placebo medications as therapeutics and Harvard recently set up a dedicated institute called "The Program in Placebo Studies and the Therapeutic Encounter."

The decoding of the placebo effect seems to be just a nascent step along the way to the more ambitious quest of mind reading. This past summer a group at UC Berkeley was able to show, via reconstructing brain imaging activation maps, a reasonable facsimile of short YouTube movies that were shown to individuals. In fact, it is pretty awe-inspiring and downright scary to see the resemblance of the frame-by-frame comparison of the movie shown and what was reconstructed from the brain imaging.

Coupled with the new initiative of developing miniature, eminently portable MRIs, are we on the way to watching our dreams in the morning on our iPad? Or, even more worrisome, potentially having others see the movies in our brain. I wonder what placebo effect that might have. 

Out of the Mouths of Babes, or, Why is the Sky Blue?

My favorite explanation is one that I sought as a boy. It is the explanation for why the sky is blue. It's a question every toddler asks, but it is also one that most great scientists since the time of Aristotle, including da Vinci, Newton, Kepler, Descartes, Euler, and even Einstein, have asked.

One of the things I like most about this explanation—beyond the simplicity and overtness of the question itself—is how long it took to arrive at correctly, how many centuries of effort, and how many branches of science it involves.

Unlike other everyday phenomena, such as the rising and setting sun, the color of the sky did not elicit much myth-making, even by the Greeks or Chinese. There were few non-scientific explanations for its color. It took a while for the azure sky to be problematized, but, when it was, it kept our (scientific) attention. How could the atmosphere be colored when the air before our faces is not? 

Aristotle is the first, so far as we know, to ask the question about why the sky is blue, in the treatise On Colors; his answer is that the air close at hand is clear and the deep air of the sky is blue the same way a thin layer of water is clear but a deep well of water looks black. This idea was still being echoed in the 13th century by Roger Bacon. Kepler too reinvented a similar explanation, arguing that the air merely looks colorless because the tint of its color is so faint when in a thin layer. But none of them offered an explanation for the blueness of the atmosphere. So the question actually has two, related parts: why the sky has any color, and why it has a blue color. 

In the Codex Leicester, Leonardo da Vinci, writing after 1508, noted, "I say that the blue which is seen in the atmosphere is not its own color, but is caused by the heated moisture having evaporated into the most minute, imperceptible particle, which beams of the solar rays attract and cause to seem luminous against the deep, intense darkness of the region of fire that forms a covering above them." Alas, Leonardo does not actually say why these particles should be blue either.

Isaac Newton contributed, both by asking why the sky was blue, and also by demonstrating, through his pathbreaking experiments with refraction, that white light could be decomposed into its constituent colors.

Many now-forgotten and many still-remembered scientists since Newton joined in. What might refract more blue light towards our eyes? In 1760, the mathematician Leonhard Euler speculated on the wave theory of light helping to explain why the sky is blue. The 19th century saw a flurry of experiments and observations of all sorts, from expeditions to mountaintops for observation to elaborate efforts to recreate the blue sky in a bottle—as chronicled in Peter Pesic's wonderful book, Sky in a Bottle. Countless careful observations of blueness in different locations, different altitudes, different times, were made, including with bespoke devices known as cyanometers. Horace-Benedict de Saussure invented the first cyanometer in 1789. His version had 53 sections with varying shades of blue arranged in a circle. Saussure correctly reasoned that something suspended in the air must be responsible for the blue color.  

Indeed, for a very long time, it had been suspected that something in the air modified the light and made it appear blue. Eventually it was realized that it was the air itself that did this, that the very gaseous molecules that make up air itself are essential to making it appear blue. And so, the blueness of the sky is connected to the discovery of the physical reality of atoms. The color of the sky is deeply connected to atomic theory, and even to Avogadro's number! And this in turn attracted Einstein's attention in the period from 1905 to 1910.

So, the sky is blue because the incident light interacts with the gas molecules in the air in such as fashion that more of the light in the blue part of the spectrum is scattered, reaching our eyes on the surface of the planet. All the frequencies of the incident light can be scattered this way, but the high-frequency (short wavelength) blue is scattered more than the lower frequencies in a process known as Rayleigh scattering, described in the 1870's. John William Strutt, Lord Rayleigh, who also won the Nobel Prize in physics in 1904 for the discovery of argon, demonstrated that, when the wavelength of the light is on the same order as the size of the gas molecules, the intensity of scattered light varies inversely with the fourth power of its wavelength. Shorter wavelengths like blue (and violet) are scattered more than longer ones. It's as if all the molecules in the air preferentially glow blue, which is what we then see everywhere around us.

Yet, the sky should appear violet since violet light is scattered even more than blue light. But the sky does not appear violet to us because of the final, biological part of the puzzle, which is the way our eyes are designed: they are more sensitive to blue than violet light. 

The explanation for why the sky is blue involves so much of the natural sciences: the colors within the visual spectrum, the wave nature of light, the angle at which sunlight hits the atmosphere, the mathematics of scattering, the size of nitrogen and oxygen molecules, and even the way human eyes perceive color. It's most of science in a question that a young child can ask.

Why Do Movies Move?

Movies are not smooth. The time between frames is empty. The camera records only twenty-four snapshots of each second of time flow, and discards everything that happens between frames—but we perceive it anyway. We see stills, but we perceive motion. How can we explain this? We can ask the same question about digital movies, videos, and videogames—in fact, all modern digital media—so the explanation is rather important, and one of my favorites.

Hoary old "persistence of vision" can't be the explanation. It's real, but it only explains why you don't see the emptiness between the frames. If an actor or an animated character moves between frames then—by persistence of vision—you should see him in both positions: two Humphrey Bogarts, two Buzz Lightyears. In fact, your retinas do see both, one fading out as the other comes in—each frame is projected long enough to ensure this. It's what your brain does with the retinas' information that determines whether you perceive two Bogarts in two different positions or one Bogart moving.

On its own the brain perceives the motion of an edge, but only if it moves not too far, and not too fast, from the first frame to the second one. Like persistence of vision, this is a real effect, called apparent motion. It's interesting but it's not the explanation I like so much. Classic cel animation—of the old ink on celluloid variety—relies on the apparent-motion phenomenon. The old animators knew intuitively how to keep the successive frames of a movement inside its "not too far, not too fast" boundaries. If they needed to exceed those limits, they had tricks to help us perceive the motion—like actual speed lines and a poof of dust to mark the rapid descent of Wile E. Coyote as he steps unexpectedly off a mesa in hot pursuit of that truly wily Road Runner.

Exceed the apparent motion limits—without those animators' tricks—and the results are ugly. You may have seen old school stop-motion animation—such as Ray Harryhausen's classic sword-fighting skeletons in Jason and the Argonauts—that is plagued by an unpleasant jerking motion of the characters. You're seeing double, at least—several edges of a skeleton at the same time—and correctly interpret it as motion, but painfully so. The edges stutter, or "judder," or "strobe" across the screen—the words reflect the pain inflicted by staccato motion.

Why don't live-action movies stutter? (Imagine directing Uma Thurman to stay within "not too far, not too fast" limits.) Why don't computer-animated movies a la Pixar judder? And, for contrast, why do videogames, alas, strobe horribly today? All are sequences of discrete frames. There's a general explanation that works for all three. It's called "motion blur," and it's simple and pretty.

Here's what a real movie camera does. The frame it records is not a sample at a single instant, like a Road Runner or a Harryhausen frame. Rather the camera shutter is open for a short while, called the exposure time. A moving object is moving during that short interval, of course, and is thus smeared slightly across the frame during the exposure time. It's like what happens when you try to take a long-exposure still photo of your child throwing a ball and his arm is just a blur. But a bug in a still photograph turns out to be a feature for movies. Without the blur all movies would look as jumpy as Harryhausen's skeletons—unless Uma miraculously stayed within limits.

A scientific explanation can become a technological solution. For digital movies—like Toy Story—the solution to avoid strobing was derived from the explanation for live-action: Deliberately smear a moving object across a frame along its path of motion. So a character's swinging arm must be blurred along the arc the arm traces as it pivots around its shoulder joint. And the other arm independently must be blurred along its arc, often in the opposite direction to the first arm. All that had to be done was to figure out how to do what a camera does with a computer—and, importantly, how to do it efficiently. Live-action movies get motion blur for free, but it costs a lot for digital movies. The solution—by the group now known as Pixar—paved the way to the first digital movie. Motion blur was the crucial breakthrough.

In effect, motion-blur shows your brain the path a movement is taking, and also its magnitude—a longer blur means a faster motion. Instead of discarding the temporal information about motion between frames, we store it spatially in the frames as a blur. A succession of such frames overlapping a bit—because of persistence of vision—thus paints out a motion in a distinctive enough way that the brain can do the full inference.

Pixar throws thousands of computers at a movie—spending sometimes more than thirty hours on a single frame. On the other hand, a videogame—essentially a digital movie restricted to real time—has to deliver a new frame every thirtieth of a second. It was only seventeen years ago that the inexorable increase in computation speed per unit dollar (described by Moore's Law) made motion-blurred digital movies feasible. Videogames simply haven't arrived yet in 2012. They can't compute fast enough to motion blur. Some give it a feeble try, but the feel of the play lessens so dramatically that gamers turn it off and suffer the judder instead. But Moore's Law still applies, so soon—five years? ten?—even videogames will motion blur properly and fully enter the modern world.

Best of all, motion blur is just one example of a potent general explanation called The Sampling Theorem. It works when the samples are called frames, taken regularly in time to make a movie, or when they are called pixels, taken regularly in space to make an image. It works for digital audio too. In a nutshell, the explanation of smooth motion from unsmooth movies expands to explain the modern media world—why it's even possible. But that would take a longer explanation.

Mother Nature's Laws

"Deep, elegant, or beautiful explanation" requires something equally singular to explain. That means laws, by which I simply mean generalities or patterns. Thus, the "law of gravity" is general enough to describe pendulums and planets. Pendulums do not quicken my heart, but living things fascinate me, even if I have yet to express affection for nematodes.Writing from Sarawak, Alfred Wallace nailed the most important law of living things in a crisp 18 words:

Every species has come into existence coincident both in space and time with a pre-existing closely allied species.

With judicious editing, Wallace could have fit his 1855 "laws of evolution" paperinto today's word limits of PNAS or Nature. We don't find trilobites scattered in the Devonian, Jurassic, and Eocene with nothing in between. Nor are polar bears only in Greenland, Patagonia, and Tibet. The paper screams for an explanation of these bundled generalities of palaeontology and biogeography.

The scientific community were asleep at the wheel and barely noticed. A few years later, that forced Wallace to send his deep, elegant and very beautiful explanation to Darwin for moral support. Darwin had the same explanation of course. The resulting and familiar history is not where I want to go with this.

What other laws has Mother Nature given us for biological diversity?

The average geographical range size of a group of species is very much larger than the median range.

The average of the geographical ranges of 1684 species of mammals in the New World is 1.8 million km², but 50% of those species have ranges smaller than 250,000 km²—a seven to one ratio. For the region's three main bird groups, the ratio is five and eight times and for amphibians, forty times. There are many species with small ranges and few with large ranges.

There are more species in the tropics than temperate regions.

The first explorers to reach the tropics uncovered this law. Rembrandt was painting birds of paradise and marine cone shells in the early 1600s. Wallace went first to the Amazon because collecting novel species was how he earned a living.

Species with small ranges concentrate in places that typically are not where the largest numbers of species live.

This just doesn't make sense. Surely, with more species, one should have more species with large ranges, small ranges, and everything in between. It isn't so. Small-ranged species concentrate in some very special places. About half of all species live in a couple dozen places that together constitute about 10% of the ice-free parts of the planet.

Species with small ranges are rare within those ranges, while those with large ranges are common.

Pardon the language, but Mother Nature is a bitch. You'd think she'd give species with small ranges a break—and make them locally common. Not so. Widespread species tend to be common everywhere, while local ones are rare even where you find them.

What inspired Darwin and Wallace were encounters with places rich in birds and mammals found nowhere else—the Galapagos and the islands in southeast Asia. There are no such places in Europe. Darwin spent most of HMS Beagle's voyage too far south in South America, while Wallace's first trip was to the Amazon. The Amazon is very rich in species, but it is a striking example of the law that such places rarely have many species with small ranges. (I suspect this cost Wallace dearly because his sponsors wanted novelty. He found that on his next trip, to the East.)

Scientists found widespread species first. Darwin and Wallace were among the first explorers to encounter the majority of species—those with small, geographical ranges concentrated in a few places. Even for well-known groups of species, those with the smallest ranges have only been discovered in the last decades.

What deep, elegant, and beautiful explanation underpins these ineluctably connected laws? There isn't one.

Given the observed distribution of range sizes, the tropics have to have more species simply because there are in the middle. Sufficiently large ranges must span the middle—that's the only way to fit them in. But, they need not be at the ends—which geographically tend to be arctic or temperate places. Yet, middles have more species than ends even when the middles are not tropical. There are more species in the middle of Madagascar's wet forests, though it's the northern end (with fewer species) that is closer to the equator, for example.

In addition, warm, wet middles—tropical moist forests—have more species than hotter and drier middles. The correlation of species with warmth and wetness is compelling, but a compelling mechanism is illusive.

Small-ranged species can be anywhere—near middles or near ends. They are not. They tend to be on islands (Galapagos, southeast Asia), and on "habitat islands"—mountaintops—(the Andes). This fits our ideas on how species form. Alas, they are not on temperate islands and mountains, so Darwin and Wallace had to leave home to be inspired. Except for salamanders: the Appalachians of the Eastern USA seem to have different species under every rock, forming an a theoretically obstinate temperate centre of endemism that isn't matched by birds, mammals, plants, or indeed other amphibians.

To make matters worse, all this assumes that we know why some species have large ranges and more have small. We do not.

In short, we have correlations, special cases, and some special pleading, but elegance is missing. A deep explanation need not be there, of course. Our ignorance hurts.

Concentrations of local, rare species are where human actions drive species to extinction one hundred to one thousand times faster than the natural rate. Yes, we can map birds and mammals and so know where we need to act to save them. But not butterflies, which people love, let alone nematodes. Without explanations, we cannot tell whether the places we protect birds will also protect butterflies. Unless we understand Mother Nature's Laws and can extend them to the great majority of species still unknown to science, we may never know what we destroyed. 

We Are What We Do

My favorite is the idea that people become what they do. This explanation of how people acquire attitudes and traits dates back to the philosopher Gilbert Ryle, but was formalized by the social psychologist Daryl Bem in his self-perception theory. People draw inferences about who they are, Bem suggested, by observing their own behavior.

Self-perception theory turns common wisdom on its head. People act the way they do because of their personality traits and attitudes, right? They return a lost wallet because they are honest, recycle their trash because they care about the environment, and pay $5 for a caramel brulée latte because they like expensive coffee drinks. While it is true that behavior emanates from people's inner dispositions, Bem's insight was to suggest that the reverse also holds. If we return a lost wallet, there is an upward tick on our honesty meter. After we drag the recycling bin to the curb, we infer that we really care about the environment. And after purchasing the latte, we assume that we are coffee connoisseurs.

Hundreds of experiments have confirmed the theory and shown when this self-inference process is most likely to operate (e.g., when people believe they freely chose to behave the way they did, and when they weren't sure at the outset how they felt).

Self-perception theory is an elegant in its simplicity. But it is also quite deep, with important implications for the nature of the human mind. Two other powerful ideas follow from it. The first is that we are strangers to ourselves. After all, if we knew our own minds, why would we need to guess what our preferences are from our behavior? If our minds were an open book, we would know exactly how honest we are and how much we like lattes. Instead, we often need to look to our behavior to figure out who we are. Self-perception theory thus anticipated the revolution in psychology in the study of human consciousness, a revolution that revealed the limits of introspection.

But it turns out that we don't just use our behavior to reveal our dispositions—we infer dispositions that weren't there before. Often, our behavior is shaped by subtle pressures around us, but we fail to recognize those pressures. As a result, we mistakenly believe that our behavior emanated from some inner disposition. Perhaps we aren't particularly trustworthy and instead returned the wallet in order to impress the people around us. But, failing to realize that, we infer that we are squeaky clean honest. Maybe we recycle because the city has made it easy to do so (by giving us a bin and picking it up every Tuesday) and our spouse and neighbors would disapprove if we didn't. Instead of recognizing those reasons, though, we assume that we should be nominated for the Green Neighbor of the Month Award. Countless studies have shown that people are quite susceptible to social influence, but rarely recognize the full extent of it, thereby misattributing their compliance to their true wishes and desires--the well-known fundamental attribution error.

Like all good psychological explanations, self-perception theory has practical uses. It is implicit in several versions of psychotherapy, in which clients are encouraged to change their behavior first, with the assumption that changes in their inner dispositions will follow. It has been used to prevent teenage pregnancies, by getting teens to do community service. The volunteer work triggers a change in their self-image, making them feel more a part of their community and less inclined to engage in risky behaviors. In short, we should all heed Kurt Vonnegut's advice: "We are what we pretend to be, so we must be careful about what we pretend to be."

General Relativity 

General relativity is one example of a beautiful explanation of the way nature works. In fact I would argue that it is a truly extraordinary example because it is beautiful in three distinct ways. However, there's an ugly truth that we also have to consider: the concept of beauty is notoriously subjective.

First, general relativity is beautiful in the mathematical sense. Like a great work of art, it is built on strong, basic, foundations that are free of superfluous adornments. Einstein used a handful of principles to blend two fundamental concepts that had, until he came along, been thought to be independent: space and time, on the one hand, and matter and motion on the other.

The quest for this kind of beauty carries a distant echo of the Aesthetic Movement's battle cry of 'art for art's sake'. Distant, yes, but also distinct and pervasive. Bertrand Russell once said that mathematics had a cold and austere beauty, "like that of sculpture." In his book, A Mathematician's Apology, G. H. Hardy suggests that a beautiful proof possesses "inevitability", "unexpectedness", and "economy". Others talk of universality, simplicity, and elemental power. 

The great Paul Dirac admired general relativity more than any other modern theory (much more than quantum mechanics). He found it as spine-tinglingly inspirational as any great work of music. That is because he valued aesthetic appeal to an extraordinary degree. At a seminar in Moscow in 1956, when asked to summarise his philosophy of physics, Dirac had once scribbled on the blackboard in capital letters, "Physical laws should have mathematical beauty."

But there's another sense in which theories are beautiful. In his award-winning biography of Dirac, The Strangest Man, Graham Farmelo, describes a telling encounter, recorded by the BBC, between Dirac and his friend Werner Heisenberg, when the latter had made the pragmatic, and apparently uncontroversial, remark that beauty is less important than agreement with experimental results.

Dirac countered with the example of another friend, Erwin Schrödinger, whom Dirac greatly admired for his appreciation of mathematical beauty, and whose eponymous equation describes the behaviour of matter in the micro-world of atoms and molecules. He had attempted to formulate versions of the Schrödinger equation that were compatible with special relativity and gave up when he realised this equation (now called the Klein-Gordon equation) gave incorrect results when used to calculate the energy levels of hydrogen.

Dirac pointed out that if Schrödinger had shown more faith in beauty, he would have ended up publishing the first relativistic version of quantum theory. Heisenberg conceded there was indeed a value to being aesthetic (Farmelo remarks: "Dirac's face lit up with the broadest of smiles, revealing two rows of rotting teeth.")

But Heisenberg gave up too easily. There is indeed another, important, sense in which a theory is beautiful, as Heisenberg himself knew only too well. There are plenty of 'beautiful' theories out there that lack relevance: tellingly, Einstein had become obsessed by this ultra-pure form of beauty towards the end of his career, when he was much less creative. He had lost sight of something important. The most elegant theories of all also possess the beauty of utility: in this sense, general relativity has incredible allure. It gives a dazzling account of gravity.

 I would like to argue that there is yet another dimension to the beauty of utility, which goes beyond giving an immaculate account of how nature works. General relativity is also beautiful because it is a fecund theory. It does more than 'give a great account of gravity' – it has yielded new insights in nature, revealing novel vistas that have enabled theorists to keep well ahead of experimenters for decades. Einstein and the likes of Hawking, Penrose, Chandrasekhar and many more used it to shed light on extraordinary phenomena, from the Big Bang 13.7 billion years ago to gravitational waves to the stability of stars to the properties of black holes.

 Beautiful bottom line: the supreme fundamental theories should be elegant at the mathematical level, offer a precise fit with nature and also open up new worlds of intellectual endeavour.

 One ugly fact remains, however: subjectivity. Why is it that mathematics provides the most beautiful depictions of nature that we have? We all assume this is true but we don't know for sure. It seems that the greatest engine of cultural change—the scientific world-view—rests on a foundation that, in some respects, is ultimately religious. Today it has become a cliché to say that, as Dirac put it in a Scientific American article in 1963: "God is a mathematician of a very high order." God's alleged aestheticism is an illusion, however. I put my faith in mathematical physicists. They are on the right path to a profound and objective truth, the beautiful details of which have yet to be revealed in full.  

We Are Enslaved Not By What We Fear, But By What We Love

George Orwell's Big Brother taught us what we need to know about authoritarian forms of social control. Mount perpetual war and call it peace. Debase language. Efface memory. Surround people with screens broadcasting propaganda and, at the same time, use these screens for surveillance.

But what if the screens that surround us are not objects of fear, but things we desire? What if propaganda and surveillance are delivered through the mediated images we crave?

This opposing model of social control—where we are enslaved not by what we fear, but by what we love—was described in 1932 by Aldous Huxley, George Orwell's former teacher at Eton. In Huxley's Brave New World, people delight in celebrity culture, sex tapes, recreational drugs, elaborate games, and pornographic films designed to rev up audiences for their own promiscuous pairings. 

Orwell and Huxley recognized the same historical amnesia, illiteracy, and debasement of language. They identified similar hierarchies of social control and propaganda regimes, enforced by surveillance.  But one world was ruled by fear, the other by love—or at least the simulated desire that today passes for love. As we delight in our screens and the happy images that bathe us in their networked glow, our pleasures present one of today's greatest perils.  

Gravity Is Curvature Of Spacetime … Or Is It?

My favorite elegant explanation is probably wrong—but is deeply powerful nonetheless. It is: gravity is curvature of spacetime.

This central idea has shaped our ideas of modern cosmology, given us the image of the expanding universe, and has led to remarkable understandings—such as the apparent presence of a black hole four million times the mass of the sun at the center of our galaxy. It even offers a possible explanation of the origin of our Universe—as quantum tunneling from "nothing."

This idea lies at the heart of Einstein's General Theory of Relativity, which is still our best understanding of gravity, after nearly 100 years. Its essence is embodied in Wheeler's famous words: "matter tells spacetime how to curve, and curved spacetime tells matter how to move" The equations expressing this are even simpler, once one has understood the background math. The theory exudes simple, essential beauty.

But when brought together with quantum mechanics, an epic conflict between the two theories results. Apparently, they both cannot be right. And, the lessons of black holes—and Hawking's discovery that they ultimately explode—seem to teach us that quantum mechanics must win, and classical spacetime is doomed.

We do not yet know the full shape of the quantum theory providing a complete accounting for gravity. We do have many clues, from studying the early quantum phase of cosmology, and ultrahigh energy collisions that produce black holes and their subsequent disintegrations into more elementary particles. We have hints that the theory draws on powerful principles of quantum information theory. And, we expect that in the end it has a simple beauty, mirroring the explanation of gravity-as-curvature, from an even more profound depth. 

My Most Flavorful Explanation. Would You Like Blue Cheese With It?

It would take about 100 years to try the 100,000 recipes carried on Epicurious, the largest recipe portal in the US.What fascinates me about this number is not how huge it is, but rather how tiny. Indeed, a typical dish has about eight ingredients. Thus the roughly 300 ingredients used in cooking today allow for about 1,000,000,000,000,000distinct dishes. Add to this your choice of deep freezing, frying, smashing, centrifuging, or blasting your ingredients, and you start to see why cooking is a growth industry. It currently uses only a negligible fraction of its resources—less than one in a trillion dishes that culinary combinatorics permits.

Don't you like green eggs and ham? Or why leave this vast terra incognita unexplored? Do we simply lack the time to taste our way through this boundless bounty, or is it because most combinations are repugnant anyway? Could there be some rules that explain liking some ingredient combinations and avoiding others? The answer appears to be yes, which leads me to my most flavorful explanation to date.

As we search for evidence to support (or refute) any 'laws' that may govern our culinary experiences, we must bear in mind that food sensation is affected by many factors, from color to texture, from temperature to even sound. Yet palatability is largely determined by flavor, representing a group of sensations including odors, tastes, freshness and pungency. This is mainly chemistry, however. Odors are molecules that bind olfactory receptors, tastes are chemicals that stimulate taste buds, freshness or pungency are driven by chemical irritants in our mouth and throat. Therefore, if we want to understand why we prize some ingredient combinations and loathe others, we have to look at the chemical profile of our recipes.

But how can chemistry tell us which ingredients taste well together? Well, we can formulate two orthogonal hypotheses. First, we may like some ingredients together because their chemistry (and henceforth their flavor) is complementary—what one lacks, is provided by the other. The alternative is its polar opposite: taste is like color matching in fashion—we prefer to pair ingredients that already share some flavor compounds, bringing them in chemical harmony with each other. Before you go on reading, I urge you to stop for a second and ponder which of these would you find more plausible.

To this day, it is the first one that makes more sense to me: I put salt in my omelet not because the chemical bouquet of the egg shares the salt's only chemical, NaCl, but precisely because it is missing it. Yet, lately chefs and molecular gastronomers are betting on the second hypothesis, and they even gave it a name, calling it the food pairing principle. Its consequences are already on your table: some contemporary restaurants serve white chocolate with caviar, as they share trimethylamine and other flavor compounds, or chocolate and blue cheese that share at least 73 flavor compounds. Yet, evidence for food pairing is at best anecdotal, making a scientist like myself ask: is this more than a myth?

So whom should I trust, my intuition or the molecular gastronomers? And how to really test if two ingredients indeed go well together? Our first instinct was to taste under controlled conditions all ingredient pairs. Yet 300 ingredients offer about 44,850 pairs to sample, forcing us to search for smarter ways to settle the question. Having spent the last decade trying to understand the laws governing networks, from the social network to the intricate web of genes governing our cells, we decided to rely on network science. We therefore compiled the flavor components of over 300 ingredients and organized them into a network, linking two ingredients if they share flavor compounds. We then used the collective intelligence accumulated in the existing body of recipes to test what goes with what. If two common ingredients are almost never combined, like garlic and vanilla, there must be a reason for it—those who tried it, may have found it either uninspired or outright repulsive. If, however, two ingredients are more often together than we would expect based on their individual popularity, we took that as a sign that they must taste well together. Tomato and garlic are in this category, combined in 12 percent of all recipes.

The truth is rather Dr. Seussian at the end: we may like some combinations here, but not there. That is, North American and Western European cuisine show a strong tendency to combine ingredients that share chemicals. Hence, color matching dominates much of the western cuisine. If you are here, serve parmesan with papaya and strawberry with beer. Do not try this there, however: East Asian cuisine thrives through avoiding ingredients that share favor chemicals. So if you hail from Asia, yin yang is your guiding force: seeking harmony through pairing the polar opposites. Do you like soy sauce with honey? Try them and you may, I say. 

Observers Observing

Hormesis Is Redundancy

Nature is the master statistician and probabilist. It follows a certain logic based on layers of redundancies, as a central risk-management approach. Nature builds with extra spare parts (two kidneys), and extra capacity in many, many things (say lungs, neural system, arterial apparatus, etc.), while design by humans tend to be spare, overoptimized, and have the opposite attribute of redundancy, that is, leverage—we have a historical track record of engaging in debt, which is the reverse of redundancy (fifty thousand in extra cash in the bank or, better, under the mattress, is redundancy; owing the bank an equivalent amount is debt).

Now, remarkably, the mechanism called hormesis is a form of redundancy and statistically sophisticated in ways human science (so far) has failed us.

Hormesis is when a bit of a harmful substance, or stressor, in the right dose or with the right intensity, stimulates the organism and makes it better, stronger, healthier, and prepared for a stronger dose the next exposure. That's the reason we go to the gym, engage in intermittent fasting, or caloric deprivation, or overcompensate for challenges by getting tougher. Hormesis lost some scientific respect, interest and practice after the 1930s partly because some people mistakenly associated it with the practice of homeopathy. The association was unfairly done as the mechanisms are extremely different. Homeopathy relies on other principles, such as the one that minute, highly diluted parts of the agents of a disease (so small they can hardly be perceptible, hence cannot cause hormesis) could help medicate against the disease itself. It has shown little empirical backing and belongs today to alternative medicine, while hormesis, as an effect, has shown ample scientific evidence.

Now it turns out that the logics of redundancy and overcompensation are the same—as if nature had a simple elegant and uniform style in doing things. If I ingest, say, fifteen milligrams of a poisonous substance, my body will get stronger, preparing for twenty, or more. Stressing my bones (karate practice or carrying water on my head) will cause them to prepare for greater stress, by getting denser and tougher. A system that overcompensates is necessarily in overshooting mode, building extra capacity and strength, in anticipation for the possibility of a worse outcome, in response to information about the possibility of a hazard. This is a very sophisticated form of discovering probabilities via stressors. And of course such extra capacity or strength becomes useful—in itself—as opportunistic as it can be used to some benefit even in the absence of the hazard. Redundancy is an aggressive, not a defensive approach to life.

Alas, our institutional risk management methods are vastly different. Current practice is to look in the past for worst-case scenario, called "stress test" and adjust accordingly, never imagining that, just as the past experienced a large deviation that did not have a predecessor, that such deviation might be insufficient. For instance, current systems take the worst historical recession, the worst war, the worst historical move in interest rates, the worst point in unemployment, etc., as an anchor for the worst future outcome. Many of us have been frustrated—very frustrated—by the method of stress testing in which people never go beyond what has happened before and even had to face the usual expression of naive empiricism, "do you have evidence?" when suggesting that we need to consider worse.

And, of course, these systems don't do the recursive exercise in their mind to see the obvious, that the worst past event itself did not have a predecessor of equal magnitude, and that someone using the past worst case in Europe before the Great War would have been surprised. I've called it the Lucretius underestimation, after the Latin poetic philosopher who wrote that the fool believes that the tallest mountain there is should be equal to tallest one he has observed. Danny Kahneman's wrote, using as backup the works of Howard Kunreuther, that "protective actions, whether by individuals or by governments, are usually designed to be adequate to the worst disaster actually experienced (...) Images of even worse disaster do not come easily to mind." For instance, in Pharaonic Egypt, scribes have tracked the high-water mark of the Nile and used it as worst-case scenario. No economist had tested the obvious: do extreme events fall according to the past? Alas, backtesting says: no, sorry.

The same dangerous recklessness can be seen in the methodology used for the Fukushima nuclear reactor, built to the worst past outcome, and not imagining and extrapolating to much worse. Well, nature, unlike risk engineers, prepares for what has not happened before, assuming worse harm is possible.

So if humans fight the last war, nature fights the next war. Of course, there is a biological limit to our overcompensation.

This form of redundancy remains vastly more extrapolative than our minds that are intrapolative.

The great Benoit Mandelbrot, now gone for a year, saw the same fractal self-similarity in nature and in probabilities of historical and economic events. It is thrilling to see how the two domains unite under the notion of fractal-based redundancy.

p.s. The word "fitness" in the common scientific discourse does not appear to be precise enough. I am unable to figure out if what is called "Darwinian fitness" is merely intrapolative adaptation to current environment, or if it contains an element of statistical extrapolation. In other words, there is a significant difference between robustness (is not harmed by stressor) and what I've called antifragility (i.e., gains from stressors).

A Sphere

Most scientific facts are based on things that we cannot see with the naked eye or hear by our ears or feel by our hands. Many of them are described and guided by mathematical theory. In the end, it becomes difficult to distinguish a mathematical object from objects in nature.

One example is the concept of a sphere. Is the sphere part of nature or it is a mathematical artifact? That is difficult for a mathematician to say. Perhaps the abstract mathematical concept is actually a part of nature. And it is not surprising that this abstract concept actually describes nature quite accurately.

Sleep Is the Interest We Have to Pay on the Capital Which is Called In at Death

Sleep is the interest we have to pay on the capital which is called in at death; and the higher the rate
of interest and the more regularly it is paid, the further the date of redemption is postponed.

So wrote Arthur Schopenhauer, comparing life to finance in a universe that must keep its books balanced. At birth you receive a loan, consciousness and light borrowed from the void, leaving a hole in the emptiness. The hole will grow bigger each day. Nightly, by yielding temporarily to the darkness of sleep, you restore some of the emptiness and keep the hole from growing limitlessly. In the end you must pay back the principal, complete the void, and return the life originally lent you.

By focusing on the common periodic nature of sleep and interest payments, Schopenhauer extends the metaphor of borrowing to life itself. Life and consciousness are the principal, death is the final repayment, and sleep is la petite mort, the periodic little death that renews. 

Elegant = Complex

Many would say the opposite, elegance = simplicity. They have (classical) physics envy—for smooth, linear physics, and describably delicious four-letter words, like "F=ma". But modern science has moved on, embracing the complex. Occam now uses a web-enabled, fractal e-razor. Even in mathematics, stripped of awkward realities of non-ideal gases, turbulence, and non-spherical cows, simple statements about integers like Fermat’s aⁿ + bⁿ = cⁿand wrangling maps with four colors take many years and pages (occasionally computers) to prove.

The question is not "What is our favorite elegant explanation?", but "What should it be?" We are capable of changing not only our mind, but changing the whole fabric of human nature. As we engineer, we recurse—successively approximating ourselves as an increasingly survivable force of nature. If so, what will we ultimately admire? Our evolutionary baggage served our ancestors well, but could kill our descendants. Faced with modern foods, our frugal metabolisms feed a diabetes epidemic. Our love of "greedy algorithms" leads to exhausted resources. Our too easy switching from rationality to blind-faith or fear-based decision making can be manipulated politically to drive conspicuous consumption. (Think Easter Island 163 km² of devastation scaled to Earth Island at 510 million km²).  "Humans" someday may be born with bug-fixes for dozens of current cognitive biases as well as intuitive understanding and motivation to manipulate quantum weirdnesses, dimensions beyond three, super rare events, global economics, etc. Agricultural and cultural monocultures are evolutionarily bankrupt. Evolution was only briefly focused on surviving in a sterile world of harsh physics, but ever since has focused on life competing with itself. Elegant explanations are those that predict the future farther and better. Our explanations will help us dodge asteroids, solar red giant flares, and even close-encounters with the Andromeda galaxy. But most of all, we will diversify to deal with our own ever-increasing complexity.  

The Beauty In A Sunrise

This year's Edge Question is about one's personal responses to explanation. When I was first excited by physics, the depths of its explanations were compelling to me in very esoteric contexts. For example, the binding of matter, energy and space-time in General Relativity seemed (and indeed is) an extraordinarily elegant and deep explanation.

Nowadays I am even more compelled by powerful explanations that lie behind the things we see around us that are too easily taken for granted. And in thinking about the Question, I find myself drawn to a context that is experienced every day by just about everybody.

How generous is that himself the sun
—arriving truly, faithfully who goes
(never for a moment ceasing to begin
the mystery of day for someone's eyes)

Thus wrote ee cummings in the opening of his short but lyrical celebration of our star. Those words highlight a daily moment—a sunrise—whose associated human sense of (in)significance and mystery may for some be only deepened by appreciating (at least) three great explanations underlying within the experience. And each of those explanations has at least one of the qualities of depth, elegance and beauty.

If you care about such things, and (like me) live at a northern middle latitude, you will know the range of the horizon visible from your home, between (roughly) south-east and north-east, across which the point of sunrise shifts back and forth over the year, with sunrise getting later as it moves northward and the days shorten, and the motion reversing at the winter solstice. And beyond that quite complex behaviour is the simple truth of the sun's fidelity—we can indeed trust it to come up somewhere in the East every morning.

Like a great work of art, a great scientific explanation loses none of its power to inspire awe afresh whenever one contemplates it. So it is with the explanation that those daily and annual cycles of sunrises are explicable by a tilted rotating Earth orbiting the Sun, whose average axial direction can be considered fixed relative to the stars thanks to a still-mysterious conservation law.

Unlike my two other chosen explanations, this one encountered scepticism from scientists for decades. The heliocentric view of the solar system, articulated by Copernicus in the mid 16^th century, was not widely accepted until well into the 17^th century. For me, that triumph over the combination of scientific scepticism and religious hostility only adds to the explanation's appeal.

Another explanation is certainly elegant and lies behind the changing hues of the sky as the sun rises. Lord Rayleigh succeeded James Clerk Maxwell as Cavendish professor of physics at Cambridge. One of his early achievements was to deduce laws of the scattering of light. His first effort reached the right answer on an invalid foundation – the scattering of light in an elastic aether. Although the existence of such an aether wasn't shown to be a fallacy until some years later, he redid his calculations using Maxwell's deeply unifying theories of electromagnetism. 'Rayleigh scattering' is the expression of those theories in contexts where an electromagnetic wave encounters electrically polarised particles much smaller than its wavelength. The amount of scattering, Rayleigh discovered, is inversely proportional to the fourth power of the wavelength. By 1899, he had shown that air molecules themselves were powerful scatterers.

There, in one bound, is the essential explanation of why the sky is blue and why sunrises are reddened. Blue light is scattered much more by air molecules than light of longer wavelengths. The sun's disk is accordingly reddened and all the more so when seen through the long atmospheric path at sunrise and sunset. (To fully account for the effect, you also need to take into account the sun's spectrum and the visual responses of human eyes.) The pink clouds that can add so much to the beauty of a sunrise consist of comparatively large droplets that scatter the wavelengths of reddened sunlight more equally than air molecules—colourwise, what you see is what they get.

The third explanation behind a sunrise is conceptually and cosmologically the deepest. What is happening in the sun to generate its seemingly eternal light and heat? Understanding the nuclear reactions at the sun's core was just a part of an explanation that (thanks especially to Burbidge, Burbidge, Fowler and Hoyle in 1957) simultaneously allowed us to understand not only the light from many kinds of stars but also how almost all the naturally occurring chemical elements are produced throughout the universe: in chains of reactions occurring within stable and cataclysmically unstable cosmic balls of gas in their various stages of stellar evolution, driven by the shifting influences of all the fundamental forces of nature—gravity, electromagnetism and the strong and weak nuclear forces.

Edge readers know that scientific understanding enhances rather than destroys nature's beauty. All of these explanations for me contribute to the beauty in a sunrise.

Ah, but what is the explanation of beauty? Brain scientists grapple with nuclear-magnetic resonance images—a recent meta-analysis indicated that all of our aesthetic judgements seem to include the use of neural circuits in the right anterior insula, an area of the cerebral cortex typically associated with visceral perception. Perhaps our sense of beauty is a by-product of the evolutionary maintenance of the senses of belonging and of disgust. For what it's worth, as exoplanets pour out of our telescopes, I believe that we will encounter astrochemical evidence for some form of extraterrestrial organism well before we achieve a deep, elegant or beautiful explanation of human aesthetics.

A Beautiful Explanation For Why The Human Mind May Seem To Have An Elegant Explanation Even If It Doesn't

On reading "The Origin of Species" Erasmus Darwin wrote to his brother Charles in 1859: "The a priori reasoning is so entirely satisfactory to me that if the facts won't fit in, why so much the worse for the facts." Some of the facts—such as Kelvin's calculation of the age of the Earth—looked awkard for Darwin's theory at the time. But the theory of natural selection was too beautiful to be wrong. The brother was sure the troublesome facts would have to change. And so they did.

But it doesn't always work that way. Elegance can be misleading. Consider a simple mathematical example. Given the sequence 2, 4, 6, 8, what rule would you guess is operating to generate the series? There are several theoretically possible answers. One would be the simple rule: take the previous number, x, and compute x + 2. But equally valid for these data would be the much more complicated rule, take the previous number, x, and compute

-1/44 xexp3 + 3/11 xexp2 + 34/11

For the sequence as given so far, the first rule is clearly the more elegant. And if someone, let's call her Tracey, were to maintain that, since both rules both work equally well, she was going to make a personal choice of the second, we would surely think she was being deliberately contrarian and anti-elegant. Tracey Emin not Michelangelo.

But suppose now Tracey were to say: "I bet if we look a little further we shall find I was right all along." And suppose, when we do look further, we find to our surprise that the next number in the sequence is not 10, but 8.91 and the next after that not 12 but 8.67, i.e. the sequence we actually discover goes 2, 4, 6, 8, 8.91, 8.67. Then what had previously seemed the better rule would no longer fit the facts at all. Yet—surprise, surprise—the second rule would still fit nicely. In this case we should be forced to concede that Tracey's anti-elegance had won the day.

How often does the real world tease us by seeming to be simpler than it really is? A famous case is Francis Crick's 1959 theory of how DNA passes on instructions for protein synthesis using a "comma free code". As Crick wrote many years later "Naturally [we] were excited by the idea of a comma-free code. It seemed so pretty, almost elegant. You fed in the magic numbers 4 (the 4 bases) and 3 (the triplet) and out come the magic number 20, the number of amino acids." But alas this lovely theory could not be squared with experimental facts. The truth was altogether less elegant.

A tease? I'm not of course suggesting that Nature was deliberately stringing Crick along. As Einstein said, God is subtle but he is not malicious. In this case the failure of the most elegant explanation to be the true one is presumably just a matter of bad luck. And, assuming this doesn't happen often, perhaps in general we can still expect truth and beauty to go together (as no doubt many of the other answers to this Edge Question will prove).

However I believe there is one class of cases where the elegance of an untrue theory may not be luck at all; where indeed complex phenomena have actually been designed to masquerade as simple ones—or at any rate to masquerade as such to human beings. And such cases will arise just when, in the course of evolution, it has been to the the biological advantage of humans to see certain things in a particularly simple way. The designer of the pseudo-elegant explananda has not been God, but natural selection.

Here is my favorite example. Individual humans appear to other humans to be controlled by the remarkable structures we call "Minds". But the surprising and wonderful thing is that human "minds" are quite easy for others to read. We've all been doing it since we were babies, using the "folk theory" known to psychologists as "Theory of Mind" (or sometimes as "belief desire psychology"). Theory of Mind is simple and elegant, and can be understood by a two-year old. There's no question it provides a highly effective way of explaining the way people behave. And this skill at mind-reading has been essential to human survival in social groups. Yet the fact is Theory of Mind could never have worked so well unless natural selection had shaped human brains to be able to read—and to be readable by—one another in this way. Which is where the explanatory sleight of hand comes in. For, as an explanation of how the brain works, Theory of Mind just doesn't add up. It's a purpose-built over-simplified deep, elegant myth. (A myth whose inadequacy may not become apparent perhaps until those "extra numbers" are added by madness or by brain damage—contingencies which selection has not allowed for).

I find this explanation of the elegance of Theory of Mind beautiful. 

We Are Stardust

Where did we come from? I find the explanation that we were made in stars to be deep, elegant, and beautiful. This explanation says that every atom in each of our bodies was built up out of smaller particles produced in the furnaces of long-gone stars. We are the byproducts of nuclear fusion. The intense pressures and temperatures of these giant stoves thickened collapsing clouds of tiny elemental bits into heavier bits, which once fused, were blown out into space as the furnace died. The heaviest atoms in our bones may have required more than one cycle in the star furnaces to fatten up. Uncountable numbers of built-up atoms congealed into a planet, and a strange disequilibrium called life swept up a subset of those atoms into our mortal shells. We are all collected stardust. And by a most elegant and remarkable transformation, our starstuff is capable of looking into the night sky to perceive other stars shining. They seem remote and distant, but we are really very close to them no matter how many lightyears away. All that we see of each other was born in a star. How beautiful is that?

Explaining How Two Systems Of The World Can Both Be True

The situation that I am trying to explain is the existence side by side of two apparently incompatible pictures of the universe. One is the classical picture of our world as a collection of things and facts that we can see and feel, dominated by universal gravitation. The other is the quantum picture of atoms and radiation that behave in an unpredictable fashion, dominated by probabilities and uncertainties. Both pictures appear to be true, but the relationship between them is a mystery.

The orthodox view among physicists is that we must find a unified theory that includes both pictures as special cases. The unified theory must include a quantum theory of gravitation, so that particles called gravitons must exist, combining the properties of gravitation with quantum uncertainties.

I am looking for a different explanation of the mystery. I ask the question, whether a graviton, if it exists, could conceivably be observed. I do not know the answer to this question, but I have one piece of evidence that the answer may be no. The evidence is the behavior of one piece of apparatus, the gravitational wave detector called LIGO that is now operating in Louisiana and in Washington State. The way LIGO works is to measure very accurately the distance between two mirrors by bouncing light from one to the other. When a gravitational wave comes by, the distance between the two mirrors will change very slightly. Because of ambient and instrumental noise, the actual LIGO detectors can only detect waves far stronger than a single graviton. But even in a totally quiet universe, I can answer the question, whether an ideal LIGO detector could detect a single graviton. The answer is no. In a quiet universe, the limit to the accuracy of measurement of distance is set by the quantum uncertainties in the positions of the mirrors. To make the quantum uncertainties small, the mirrors must be heavy. A simple calculation, based on the known laws of gravitation and quantum mechanics, leads to a striking result. To detect a single graviton with a LIGO apparatus, the mirrors must be exactly so heavy that they will attract each other with irresistable force and collapse into a black hole. In other words, nature herself forbids us to observe a single graviton with this kind of apparatus.

I propose as a hypothesis, based on this single thought-experiment, that single gravitons may be unobservable by any conceivable apparatus.

If this hypothesis were true, it would imply that theories of quantum gravity are untestable and scientifically meaningless. The classical universe and the quantum universe could then live together in peaceful coexistence. No incompatibility between the two pictures could ever be demonstrated. Both pictures of the universe could be true, and the search for a unified theory could turn out to be an illusion.

The Origin of Money

Carl Menger's account of the origin of money is my favourite scientific explanation. It is deeply satisfying because it shows how money can develop from barter without anyone consciously inventing it. As such, it is a great example of Adam Smith's invisible hand, or what scientists now call "emergence."

Menger (1840-1921) founded the Austrian school of economics, a heterodox school of thought which is derided by many mainstream economists. Yet their accounts of the origin of money beg the very question which Menger answered. The typical mainstream economics textbook lists the problems of barter exchange, and then explains how money overcomes these problems. However, that does not really explain how money actually got started, any more than listing the advantages of air travel explains how aeroplanes were invented. As Lawrence White puts it in his book on The Theory of Monetary Institutions (1999), "one is left with the impression that barterers, one morning, suddenly became alert to the benefits of monetary exchange, and, by that afternoon, were busy using some good as money."

That, of course, is ridiculous. In Menger's account, money emerges through a series of small steps, each of which is based on self-interested choices by individual traders with limited knowledge. First, individual barterers realize that, when direct exchange is difficult, they can get what they want by indirect exchange. Rather than finding someone who both has what I want and wants what I have, I need only find someone who wants what I have. I can then trade what I have for his good, even though I don't want to consume it myself, and then trade that for something I do want to consume. In that case, I will have used the intermediate good as a medium of exchange.

Menger notes that not all goods are equally marketable. In other words, some goods are easier to trade than others. It therefore pays a trader to accumulate an inventory of highly marketable items for use as media of exchange. Other alert traders in the market catch on, and eventually the market converges on a single common medium of exchange. This is money.

Menger's theory does not merely show how money can evolve without any conscious plan; it also shows that money does not depend on legal decrees or central banks. Yet this too is often overlooked by mainstream economists. Take Michael Woodford for example. Woodford is one of the most influential academic monetary economists alive today, yet in his 2003 book Interest and Prices: Foundations of a Theory of Monetary Policy, a central bank somehow becomes part of the economy within less than a page after the initial assumptions are introduced. In other words, Woodford does not even pause for a page to consider what a banking system would look like without a central bank. Yet free banking has a long history; the first such system began in China in about 995 AD, more than 600 years before the first central bank.

Can we account for the emergence of central banking by the same invisible-hand type of explanation that Menger proposed for money? The answer depends, according to Lawrence White, on just what we mean by the term "central banking." If government sponsorship is among the defining features of a central bank, then the answer is no. In other words, the emergence of central banks cannot be accounted for entirely by market forces. At some point, deliberate state action must enter the story. The government's motives for getting involved are not hard to imagine. For one thing, exclusive supply of banknotes gives the government a source of monopoly profits in the form of a zero-interest loan from the public's holding of these non-interest bearing notes.

In these troubled times, when central banks are expanding the stock of high-powered money through massive quantitative easing, Menger's theory is more relevant than ever. It alerts us to the possibility that the response to the current crisis in the eurozone need not be ever more centralization, but could instead consist of a move in the opposite direction, towards a regime in which any bank is free to issue its own banknotes, and market forces—not central banks—control the money supply.

Implications of Ivan Pavlov's Great Discovery

It's easy to imagine a politician's objecting to federal funds going to study how dogs drool. But failing to support such research would have been very short sighted indeed during the days of the great Russian physiologist Ivan Pavlov (1849—1936). As part of his Nobel Prize-winning research on digestion, he measured the amount of saliva produced when dogs were given food. In the course of this work, he and his colleagues noticed something unexpected: The dogs started to salivate well before they were fed. In fact, they salivated when they first heard the approaching footsteps of the person coming to feed them. That core observation led to the discovery of classical conditioning.

The key idea behind classical conditioning is that a neutral stimulus (such as the sound of approaching footsteps) comes to be associated with a stimulus (such as food) that reflexively produces a response (such as salivation)—and, after awhile, the neutral stimulus comes to elicit the response produced reflexively by the paired stimulus. To be clear about the phenomenon, we'll need to take a few words to explain the jargon. The neutral stimulus becomes "conditioned," and hence is known as the "conditioned stimulus" (CS), whereas the stimulus that reflexively produces the response is known as the unconditioned stimulus (UCS). And the response that is produced by the UCS is called the unconditioned response (UR). Classical conditioning occurs when the CS is presented right before a UCS, so that after a while the CS by itself produces the response. When this occurs, the response is called a conditioned response (CR). In short, at the outset a UCS (such as food) produces a UCR (such as salivation); when a CS (the sound of the feeder's footsteps) is presented before the UCS, it soon comes to produce the response, a CR (salivation), by itself.

This simple process gives rise to a host of elegant and non-intuitive explanations.

For example, consider accidental deaths from drug overdoses. In general, a narcotics user tends to take the drug in a specific setting, such as in his or her bathroom. The setting initially is a neutral stimulus, but after a person takes narcotics in it a few times, the bathroom comes to function as a CS: As soon as the user enters his or her bathroom with narcotics, the user's body responds to the setting by preparing for the ingestion of the drug. Specific physiological reactions allow the body to cope with the drug, and those reactions become conditioned to the bathroom (in other words, the reactions become a CR). To get a sufficient "high," the user must now take enough of the narcotic to overcome the body's preparation. But if the user takes the drug in a different setting, perhaps in a friend's bedroom during a party (and hence the new setting is not a CS), the CR does not occur—the usual physiological preparation for the narcotic does not take place. Thus, the usual amount of the drug functions as if it were a larger dose, and may be more than the user can tolerate without the body's preemptive readiness. Hence, although the process of classical conditioning was formulated to explain very different phenomena, it can be extended directly to explain why drug overdoses sometimes accidentally occur when usual doses are taken in new settings.

By the same token, classical conditioning plays a role in the placebo effect: For those of us who have regularly used analgesics such as ibuprofen or aspirin, such medicines begin to have their effects well before their active ingredients actually have time to take effect. How? From previous experience, the mere act of taking that particular pill has become a CS, which triggers the pain-relieving processes invoked by the medicine itself (and those processes have become a CR).

Classical conditioning also can result from an implanted defibrillator, or "pacemaker." When the heart beats too quickly, this device shocks it and thereby causes it to revert to beating at a normal rate. Until the shock level is properly calibrated, the shock can be very uncomfortable and can function as a UCS that produces fear as a UCR. Because the shock does not occur in a consistent environment, the person associates random aspects of the environment with it—which then function as CSs. And when any of those aspects of the environment are subsequently present, the person can experience severe anxiety, awaiting the possible shock and resulting reaction.

This same process explains why you would find a particular food unappealing if you happen to have eaten it and gotten food poisoning (and thus had significant gastrointestinal problems—the UCR to the UCS of tainted food). That type of food can thus come to function as a CS, and if you eat it—or even think about eating it—you may feel queasy, a CR. You may find yourself avoiding that food, and thus a food aversion is born. In fact, simply pairing pictures of particular types of food (such as French fries) with aversive photographs (such as of a horribly burned body) can change how appealing you find that food.

These examples should be sufficient to give you a sense of how the explanation for anticipatory salivation can be easily and simply extended to a wide range of phenomena. But, that said, we need to point out that Pavlov's original conception of classical conditioning was not quite right; he thought that sensory input was directly connected to specific responses, which led the stimuli to produce the response automatically. We now know that the connection is not so direct; classical conditioning involves many cognitive processes, such as attention and those that underlie the ability to interpret and understand. In fact, classical conditioning is a form of "implicit learning." As such, it allows us to navigate through life with less cognitive effort (and stress) than would otherwise be required. Nevertheless, this sort of conditioning has byproducts that can be powerful, surprising, and even sometimes dangerous.

"Power Tends To Corrupt, And Absolute Power Corrupts Absolutely."

I hope I will not be drummed out of the corps of Social Science if I confess to the fact that I can't think of an explanation in our field that is both elegant and beautiful. Perhaps deep . . . I guess we are still too young to have explanations of that sort . . . But there is one elegant and deep statement (which, alas, is not quite an "explanation") that comes close to fulfilling the criteria, and that I find very useful as well as beautifully simple.

I refer to the well-known lines Lord Acton wrote in a letter from Naples in 1887 to the effect that: "Power tends to corrupt, and absolute power corrupts absolutely." At least one philosopher of science has written that on this sentence an entire science of human beings could be built.

I find that the sentence offers the basis for explaining how a failed painter like Adolph Hitler and a failed seminarian like Joseph Stalin could end up with the blood of millions on their hands; or how the Chinese emperors, the Roman popes, or the French aristocracy failed to resist the allure of power. When a religion or ideology becomes dominant, the lack of controls will result in widening spirals of license leading to degradation and corruption.

It would be nice if Acton's insight could be developed into a full-fledged explanation before the hegemonies of our time, based on blind faith in science and the worship of the Invisible Hand, follow former forms of power in the dustbins of history.

The Importance of Individual Human Beings

I consider myself a scientist, and the theory of evolution is central to my thinking. I am a social scientist and have been informed by insights from many social sciences including economics. Yet I have little sympathy with hegemonic attempts to explain all human behaviors via evolutionary psychology, via rational choice economics and/or by a combination of these two frameworks.

In a planet occupied now by seven billion inhabitants, I am amazed by the difference that one human being can make. Think of classical music without Mozart or Stravinsky; of painting without Caravaggio, Picasso or Pollock; of drama without Shakespeare or Beckett. Think of the incredible contributions of Michelangelo or Leonardo, or, in recent times, the outpouring of deep feeling at the death of Steve Jobs (or, for that matter, Michael Jackson or Princess Diana). Think of human values in the absence of Moses or Christ.

Alas, not all singular individuals make a positive difference. The history of the 20th century would be far happier had it not been for Hitler, Stalin, or Mao (or the 21st century without Bin Laden). But in reaction to these individuals, there sometimes arises more praiseworthy figures: Konrad Adenauer in Germany, Mikhail Gorbachev in the Soviet Union, Deng Xiaoping in China. These successors also make a signal difference.

I consider Mahatma Gandhi to be the most important human being of the last millennium. His achievements in India speak for themselves. But even if Gandhi had not contributed vital energy and leadership to his own country, he had incredible influence on peaceful resisters across the globe: Nelson Mandela in South Africa, Martin Luther King Jr., in the United States, and the solitary figures in Tian-an-men Square in 1989 and in Tahrir Square in 2001.

Despite the laudatory efforts of scientists to ferret out patterns in human behavior, I continue to be struck by the impact of single individuals, or of small groups, working against the odds. As scholars, we cannot and should not sweep these instances under the investigative rug. We should bear in mind anthropologist Margaret Mead's famous injunction: "Never doubt that a small group of thoughtful committed citizens can change the world. It is the only thing that ever has."

The 19th Century Explanation of the Remarkable Connection Between Electricity And Magnetism

No explanation I know of in all of recent scientific history is as beautiful or deep, or ultimately as elegant, as the 19th century explanation of the remarkable connection between two familiar, but seemingly distinct forces in nature, electricity and magnetism. It represents to me all that is the best about science: surprising empirical discoveries combined with a convoluted path to a remarkably simple and elegant mathematical framework, which then explained far more than was ever bargained for, and in the process produced the very technology that now powers modern civilization.

It all began with strange experiments with jumping frogs and electric circuits, capped by the serendipitous discovery by the self-schooled, yet greatest experimentalist of his time, Michael Faraday of a very strange connection between magnets and electric currents. It was by then well known that a moving electric charge, i.e. a current, created a magnetic field around the current that could repel or attract other magnets located nearby.

What remained an open question was whether magnets could produce any electric force on charged objects. Faraday discovered, by accident, that when he turned on or off a switch to start or stop a current, creating a magnetic field that grew or decreased with time, during the periods when the magnetic field was changing, a force would suddenly arise in a nearby wire, moving the electric charges within it to create a current.

Faraday's law of induction, as it became known, not only is responsible for the basic principle governing all electric generators, from Niagara falls to nuclear power plants, it produced a theoretical conundrum that required the mind of the greatest theoretical physicist of his time, James Clerk Maxwell to set things straight. Maxwell realized that Faraday's result implied that it was the changing magnetic field (a pictorial concept introduced by Faraday himself because he felt more comfortable with pictures than algebra) that produced an electric field that would push the charges around the wire creating a current.

But in order for mathematical symmetry in the equations governing electric and magnetic fields, this then required that a changing electric field, and not merely moving charges, would produce a magnetic field. This not only produced a set of mathematically consistent equations every physics student knows, and some love, called Maxwell's equations, which can fit on a T-Shirt, but it established the physical reality of what was otherwise a mere figment of Faraday's imagination, a field—some quantity associated with every point in space and time.

But even more than this, Maxwell realized that if a changing electric field produced a magnetic field, then a constantly changing electric field, such as that which occurs when I continue to jiggle a charge up and down, would produce a continuously changing magnetic field. But that in turn would create a continuously changing electric field, which in turn would create a continuously changing magnetic field, and so on. This field 'disturbance' would move out from the original source, the jiggling charge, at a rate that Maxwell could calculate on the basis of his equations. The parameters in these equations came from experiment—measuring the strength of the electric force between two known charges, and the strength of the magnetic force between two known currents.

From these two fundamental properties of nature, Maxwell calculated the speed of the disturbance and found out ... you guessed it, that the speed was precisely the speed that light was measured to have! Maxwell thus discovered that light is indeed a wave ... but a wave of electric and magnetic fields that moved through space at a precise speed determined by two fundamental constants in nature thus laying the basis for Einstein to come along a generation or so later and demonstrate that the constant speed of light required a revision in our notions of space and time.

So, from jumping frogs and differential equations we came up for one of the most beautiful unifications in all of physics, the unification of electricity and magnetism in a single theory of electromagnetism, and that theory explained the existence of that which allows us to observe the universe around us, namely light, and the practical implications of the theory produced the mechanisms that power all of modern civilization and the principles that govern essentially all modern electronic devices, and the nature of the theory itself produced a series of further puzzles that allowed Einstein to yield new insights into space and time!

Not bad for a set of experiments whose worth was questioned by Gladstone (or Queen Victoria—depending upon which apocryphal story one buys)—who came into Faraday's laboratory and wondered what all the fuss was about, and what use all of this experimentation was for. He (or she) was told, either: "Of what use is a newborn baby?"—or in my favorite version of the story—"Use? Why one day this will be so useful you will tax us for it!" Beauty, elegance, depth, utility, adventure, and excitement! Science at its best!

Physical Reality Could Be Hugely More Extensive Than the Patch of Space and Time Traditionally Called 'The Universe'

An astonishing concept has entered the mainstream of cosmological thought: physical reality could be hugely more extensive than the patch of space and time traditionally called 'the universe'. A further Copernican demotion may loom ahead. We've learnt that we live in just one planetary system among billions, in one galaxy among billions. But now that's not all. The entire panorama that astronomers can observe could be a tiny part of the aftermath of 'our' big bang, which is itself just one bang among a perhaps-infinite ensemble.

Our cosmic environment could be richly textured, but on scales so vast that our purview is restricted to a tiny fragment; we're not aware of the 'big picture', any more than a plankton whose 'universe' was a liter of water would be aware of the world's topography and biosphere. It is obviously sensible for cosmologists to start off by exploring the simplest models. But there is no more reason to expect simplicity on the grandest scale than in the terrestrial environment—where intricate complexity prevails.

Moreover, string theorists suspect—for reasons quite independent of cosmology—that there may be an immense variety of 'vacuum states'. Were this correct, different 'universes' could be governed by different physics. Some of what we call 'laws of nature' may in this grander perspective be local bylaws, consistent with some overarching theory governing the ensemble, but not uniquely fixed by that theory. More specifically, some aspects may be arbitrary and others not. As an analogy (which I owe to Paul Davies) consider the form of snowflakes. Their ubiquitous six-fold symmetry is a direct consequence of the properties and shape of water molecules. But snowflakes display an immense variety of patterns because each is molded by its distinctive history and micro-environment: how each flake grows is sensitive to the fortuitous temperature and humidity changes during its growth.

If physicists achieved a fundamental theory, it would tell us which aspects of nature were direct consequences of the bedrock theory (just as the symmetrical template of snowflakes is due to the basic structure of a water molecule) and which cosmic numbers are (like the distinctive pattern of a particular snowflake) the outcome of environmental contingencies. .

Our domain wouldn't then be just a random one. It would belong to the unusual subset where there was a 'lucky draw' of cosmic numbers conducive to the emergence of complexity and consciousness. Its seemingly designed or fine -tuned features wouldn't be surprising. We may, by the end of this century, be able to say, with confidence, whether we live in a multiverse, and how much variety its constituent 'universes' display. The answer to this question will, I think, determine crucially how we should interpret the 'biofriendly' universe in which we live (and which we share with any aliens who we might one day make contact with).

It may disappoint some physicists if some of the key numbers they are trying to explain turn out to be mere environmental contingencies—no more 'fundamental' than the parameters of the Earth's orbit round the Sun. But that disappointment would surely be outweighed by the revelation that physical reality was grander and richer than hitherto envisioned.

Go Small

When confronted with a question like this the tempatation is to "go big" and respond with something,say, from Einstein's theory of relativity. Instead I will go small. When Planck introduced his quantum of action h at the turn of the 20th century he realized that this allowed for a new set of natural units. For example the Planck time is the square root of Planck's constant times the garvitational constant divided by the fifth power of the speed of light. It is the smallest unit of time anyone talks about but is it a "time?" The problem is that these constants are just that. They are the same to a resting observer as to a moving one. But the time is not. I posed this as a"divinette" to my "coven" and Freeman Dyson came up with a beautiful answer. He tried to construct a clock that would measure it. Using the quantum uncertainties he showed that it would be consumed by a black hole of its ownmaking. No measurement is possible. The Planck time ain't a time or it may be beyond time.

Duchamp's "Fountain"

Marcel Duchamp's 20^th century Readymades upended art history with the same mental earthquake with which Charles Darwin illuminated biological history. Duchamp's objects moved slowly into the mainstream as they appeared to be some sort of institutional blunder, why was a urinal slotted into the history of art instead of the history of plumbing? Why was the snow shovel inside the museum instead of outside tidying the driveway? Therein lies the essence of his Readymade: an object in the wrong place that questions the aura of objects in the right place. Had the urinal been hung fifty feet away in the restroom we would never have heard of it, but misplaced it was juried, crated, photographed, cataloged, critiqued, insured, donated, dissertated, collected, positioned, lighted, cleaned, and paid for. Had his bottle rack, chocolate grinder, pharmacy bottles or other common objects been stashed away in their proper space they would have passed no mention. But by "creating" an artwork from something made for another purpose he exposed the valuation system that produced an appearance of transcendentalism. In one end went butcher scraps and out came fine sausage. 

Duchamp was from a family of artists and mastered painterly cubism prior to breaking with art tradition by designating common objects as art objects. In doing so he exchanged visual space for mental space, a swap of form and color for context and stratified meaning, making him the father of both Pop Art and Conceptual Art, the dominant forms of art today. His Readymades are technically a nominalism, a stock prop of skepticism imported or deported from letters back and forth since the 11^th century. Nominalists believe in no eternal verities or universals, just names that imagine there are and no special objects, just ones gathered by words and privileged according to the metaphysics of the time. Hence the demystifying brilliance of the Readymades.

Duchamp pushed the envelope as far as possible with the urinal prank, also known as "Fountain"—what possibly would be less likely to be regarded as art than a piss receptacle? He signed the urinal "R. Mutt," a pun on "I'm a dog," and submitted it anonymously to the 1917 Society of Independent Artists, a New York show that employed Duchamp as a juror. The bylaws required inclusion of anyone who could pony up the six buck admission, however the jury pronounced "R. Mutt's" urinal not-art, declined to include it in the catalog and hid it behind a partition. Over the next nine decades this piss-pot was the most debated event in art theory: an artist-juror rejects the fake art of his nom de plume. In a 2004 survey art professionals voted the urinal-Fountain the world's most influential piece of modern art, ahead of works by Picasso or Matisse. Copies of the urinal-Fountain are now in eleven major collections including the Centre Pompidou and the Tate Modern. 

Duchamp did not leave behind many writings instead communicating his thought through visual mischief. When he did write it was usually another spoof such as his essay "Texticles" or his bulletin "Rongwrong" that predicted the high-minded goofiness known as deconstruction decades later. His thought became popularized as "everything is art," somewhat of a misnomer as he never spoke those exact words, documents indicate it would be more accurately "everything can be regarded as art." Duchamp fell in and out of favor over his eighty-one years, but he continued the ruse ever announcing more and more preposterous things as art: "Every breath is an artwork" he explained to an interviewer a year before he passed, "I am a breather, I enjoy it tremendously." 

Beauty and Tragedy In the Mathematics of Music

Some things are too good to be true. Others are too good not to be true. The elegant correspondence between musical consonance and simple mathematical ratios is too good not to be true. The infinitely creative system of musical harmony—based on a small set of canonical intervals and chordsarises out of this correspondence.

And yet the system has a flaw—a rip or tear in the musico-mathematical universe.

The most consonant musical interval is the octave, so much so that two tones an octave apart bear the same letter name, for example, A. The next most consonant interval is the fifth (for example, A to E). If you pluck the A string on a guitar and then pluck it again while placing your finger halfway up the fingerboard (allowing only half the string to vibrate and doubling the frequency), the pitch goes up by an octave to A. If instead you place your finger one-third the way up the fingerboard (allowing only the remaining two-thirds of the string to vibrate and increasing the frequency by a factor of 3/2) the pitch goes up by a fifth to E.

On a full size piano keyboard, if you play the lowest note, A, and then go up by twelve successive fifths, you reach A again—which happens to be seven octaves higher than the lowest A. Calculating by fifths, the highest A is (3/2)¹²times the frequency of the lowest A. Calculating by octaves, the highest A is 2⁷ times the frequency of the lowest A.

It should therefore be the case that:

(3/2)¹² = 2⁷

Tragically, this is not the case: (3/2)¹²is 129.7463, while 2⁷ is 128. Close but unequal. If you tune by octaves, the fifths are out-of-tune, and vice versa.

This discrepancy—a variant of the Pythagorian comma—shatters an edifice that rests on the beautiful principle that ratio simplicity underpins musical consonance. While each interval is most purely tuned using these simple ratios (the just tuning system: 2/1 = octave, 3/2 = perfect fifth, 4/3 = perfect fourth, 5/4 = major third and 6/5 = minor third), the mathematics falls apart when these intervals interact in music.

The Pythagorian comma has haunted string players for centuries, requiring annoying adjustments. On the violin, some notes must be played slightly sharper and others flatter to dodge dissonance. The comma held back the development of keyboard instruments, in which notes cannot be adjusted while playing, thus limiting a composition to the musical key for which the instrument was tuned.

The solution to this problem is to forego mathematical purity by fudging tuning. This discovery—which emerged in various forms over a period of centuries—unleashed new creative possibilities and inspired J.S. Bach to write The Well Tempered Clavier, which traverses all major and minor keys without discriminating on the basis of dissonance.

Today, several tuning systems achieve this end. In equal tempered tuning (used in some electronic synthesizers), the octave is divided into twelve equal semitones on a logarithmic scale. In this system, each successive semitone is 2^1/12 times the frequency of the previous one. Thus a fifth is 2^7/12 or 1.498 instead of 3/2 or 1.5; the perfect fourth is 2^5/12 or 1.3348 instead of 4/3 or 1.3333; the major third is 2^4/12 or 1.2599 instead of 5/4 or 1.25; and the minor third is 2^3/12 or 1.1892 instead of 6/5 or 1.2.

By anchoring the octaves and sprinkling the error elsewhere, consonance is compromised slightly but never disturbingly. The edifice of musical harmony is preserved by systematically fudging the very mathematical system upon which it is built. An elegant way to fix inelegance in an elegant musico-mathematical system.

"There are more things in heaven and earth… than are dreamed of in your philosophy."

It doesn't sound like an explanation, but I take it that way. For me, Hamlet's admonition explains the confusion and uncertainty of the universe, (and, lately, the multiverse).  It urges us on when, as they always will, our philosophies produce anomalies. It answers the unspoken question, "WTF?" With every door into nature we nudge open, a hundred new doors become visible, each with it's own inscrutable combination lock. It's both an explanation and a challenge, because there's always more to know.

I like how it endlessly loops back on itself. Every time you discover a new thing in heaven or earth, it becomes part of your philosophy, which will eventually be challenged by new new things.

Like all explanations, of course, it has its limits. Hamlet says it to Horatio as a way of urging him to accept the possibility of ghosts. It could just as well be used to prompt belief in UFOs, astrology, and even god—as if to say that that something is proved to exist by the very fact that you can't disprove it exists.

Still, the phrase can get us places. Not as a taxi to the end of thinking, but as a passport to exploration.

I think these words of Hamlet's are best thought of as a ratchet, a word earthily beautiful in sound and meaning: Keep moving on, but preserve what works. We need Einstein for GPS, but we can still get to the moon with Newton.

Why the Greeks Painted Red People On Black Pots

An explanation of something that seems not to need explaining is good. If it leads to further explanations of things that didn't seem to need explaining, that is better. If it makes a massive stink, as academic vested interests attempt to preserve the status quo in the face of far reaching implications, it is one of the best. I have chosen Michael Vickers' simple and immensely influential explanation of why the ancient Greeks painted little red figures on their pots.

The 'red figure vase' is an icon of antiquity. The phrase is frequently seen on museum labels, and the question of why the figures were not white, yellow, purple or black—other colours the Greeks could and did produce in pottery slips and glazes—does not seem important. Practically speaking, Greek pottery buyers could mix and match without fear of clashing styles, and the basic scheme allowed the potters to focus on their real passion: narrative story telling. The black background and red silhouettes make complex scenes—mythological, martial, industrial, domestic, sporting and ambitiously sexual—graphically crisp. Anyone can understand what is going on (for which reason museums often keep their straight, gay, lesbian, group, bestial, and olisbos [dildo-themed] stuff out of public view, in study collections). So clearly there is enough about Greek vases to catch the eye without thinking about the colour scheme.

Michael's brilliance was to take an idea well known to the scholar Vitruvius in the first century BC and apply it in a fresh context. Vitruvius noted that many features of Greek temples that seemed merely decorative were a hangover from earlier practical considerations: little rows of carefully masoned cubes and gaps just under the roof line were in fact a skeuomorph or formal echo of the beam ends and rafters that had projected at that point when the structures were made of wood. Michael argued that Greek pottery was skeuomorphic too, being the cheap substitute for aristocratic precious metal. He argued that the red figures on black imitated gilded figures on silver, while the shapes of the pots, with their sharp carinations and thin, strap-like handles, so easily broken in clay, were direct translations of the silversmith’s craft.

This still seems implausible to many. But to those of us, like myself, working in the wilds of Eastern European Iron Age archaeology, with its ostentatious barbarian grave mounds packed with precious metal luxuries, it made perfect sense. Ancient silver appears black on discovery, and the golden figuration is a strongly contrasting reddish gold. Museums typically used to 'conserve' such vessels, not realising that (as we now know) the sulfidized burnish to the gold was deliberate, and that no Greek would have been seen dead with shiny silver (a style choice of the hated Persians, who flaunted their access to the exotic lemons with which they cleaned it).

For me, an enthusiast from the start, the killer moment was when Michael photographed a set of lekythoi, elegant little cylindrical oil or perfume jars, laid down end to end in decreasing order in an elegant curve. He demonstrated thereby that no lekythos (the only type of major pottery with a white background, and black only for base and lid) had a diameter larger than the largest lamellar cylinder that could be obtained from an elephant tusk. These vessels, he explained, were skeuomorphs of silver-mounted ivory originals.

The implications are not yet settled, but the reputation of ancient Greece as a philosophically-oriented,  art-for-art's sake culture can now be contrasted with an image of a world where everyone wanted desperately to emulate the wealthy owners of slave-powered silver mines with their fleets of trade galleys (in my view, the scale of the ancient economy in every dimension—slavery, trade, population levels, social stratification—has been systematically underestimated, and with it the impact of colonialism and emergent social complexity in prehistoric Eurasia).

The irony for the modern art world is that the red figure vases that change hands for vast sums today are not what the Greeks themselves actually valued. Indeed, it is now clear that the illusion that these intrinsically cheap antiquities were the real McCoy was deliberately fostered, through highly selective use of Greek texts by nineteenth century auction houses intent on creating a market.

Tit For Tat

Selfishness can sometimes seem like the best strategy. It is the rational response to the prisoner's dilemma, for instance, where each individual in a pair can either cooperate or defect, leading to four potential outcomes. No matter what the other person does, selfish behavior always yields greater return. But if both players defect, both do worse than if they had cooperated. Yet when political scientist Robert Axelrod and his colleagues ran hundreds of rounds of the prisoner's dilemma on a computer, the repetition of the game led to a different result.

Experts from a wide range of disciplines submitted 76 different game strategies for Axelrod to try—some of them very elaborate. At the end of 200 rounds, one strategy was far more successful than the others. It was also the simplest. Tit For Tat, a scheme where the player cooperates on the first move and thereafter does what was done on the previous move, was the winner. The importance of cooperation to evolution was detected by humans, but simulated and verified with machines.

This elegant explanation was then documented in living egoists with an elegant experiment. Evolutionary biologist Manfred Milinski noticed Tit For Tat behavior in his subjects, three-spined sticklebacks (Gasterosteus aculeatus). When he watched a pair of these fish approach a predator, he observed four options: they could swim side by side, one could take the lead while the other followed closely behind (or vice versa), or they could both retreat. These four scenarios satisfied the four inequalities that define the prisoner's dilemma. 

For the experiment, Milinski wanted to use pairs of sticklebacks, but they are impossible to train. So he placed in the tank a single stickleback and a set of mirrors that would act like two different types of companions. In the first treatment, a parallel mirror was used to simulate a cooperative companion that swam alongside the subject stickleback. In the second treatment, an oblique mirror system set at a 32-degree angle simulated a defecting partner—that is, as the stickleback approached the cichlid, the companion appeared to fall increasingly and uncooperatively behind. Depending on the mirror, the stickleback felt he was sharing the risk equally or increasingly going it alone.

When the sticklebacks were partnered with a defector, they preferred the safer half of the tank furthest away from the predator. But in the trials with the cooperating mirror, the sticklebacks were two times more likely to venture into the half of the tank closest to the cichlid. The sticklebacks were more adventurous if they had a sidekick. In nature, cooperative behavior would translate to more food, more space, and therefore greater individual reproductive success. Contrary to predictions that selfish behavior or retreat was optimal, Milinski's observation that sticklebacks most often approached the predator together was in line with Axelrod's conclusion that Tit For Tat was the optimal evolutionary strategy.

Milinski's evidence, published in 1987 in the journal Nature, was the first to demonstrate that cooperation based on reciprocity definitely evolved among egoists, albeit small ones. A large body of research now shows that many biological systems, especially human societies, are organized around various cooperative strategies; the scientific methods continue to become more and more sophisticated, but the original experiments and Tit For Tat strategy are beautifully simple.

Boltzmann's Explanation Of The Second Law Of Thermodynamics

"What is your favorite, deep, elegant, or beautiful explanation?" That's a tough question for a theoretical physicist; theoretical physics is all about deep, elegant, beautiful explanations; and there are just so many to choose from.

Personally my favorites are explanations that that get a lot for a little. In physics that means a simple equation or a very general principle. I have to admit though, that no equation or principle appeals to me more than Darwinian evolution, with the selfish gene mechanism thrown in. To me it has what the best physics explanations have: a kind of mathematical inevitability. But there are many people who can explain evolution much better than I, so I will stick to what I know best.

The guiding star for me, as a physicist, has always been Boltzmann's explanation of second law of thermodynamics: the law that says that entropy never decreases. To the physicists of the late 19^th century this was a very serious paradox. Nature is full of irreversible phenomena: things that easily happen but could not possibly happen in reverse order. However, the fundamental laws of physics are completely reversible: any solution of Newton's equations can be run backward and it is still a solution. So if entropy can increase, the laws of physics say it must be able to decrease. But experience says otherwise. For example, if you watch a movie of a nuclear explosion in reverse, you know very well that it's fake. As a rule, things go one way and not the other. Entropy increases.

What Boltzmann realized is that the second law—entropy never decreases—is not a law in the same sense as Newton's law of gravity, or Faraday's law of induction. It's a probabilistic law that has the same status as the following obvious claim; if you flip a coin a million times you will not get a million heads. It simply won't happen. But is it possible? Yes, it is; it violates no law of physics. Is it likely? Not at all. Boltzmann's formulation of the second law was very similar. Instead of saying entropy does not decrease, he said entropy probably doesn't decrease. But if you wait around long enough in a closed environment, you will eventually see entropy decrease: by accident, particles and dust will come together and form a perfectly assembled bomb. How long? According to Boltzmann's principles the answer is the exponential of the entropy created when the bomb explodes. That is a very long time, a lot longer than the time to flip a million heads in a row.

I'll give you a simple example to see how it is possible for things to be more probable one way than the other, despite both being possible. Imagine a high hill that comes to a narrow point—a needle point—at the top. Now imagine a bowling ball balanced at the top of the hill. A tiny breeze comes along. The ball rolls off the hill and you catch it at the bottom. Next, run it in reverse: the ball leaves your hand, rolls up the hill, and with infinite finesse, comes to the top—and stops! Is it possible? It is. Is it likely? It is not. You would have to have almost perfect precision to get the ball to the top, let alone to have it stop dead-balanced. The same is true with the bomb. If you could reverse every atom and particle with sufficient accuracy, you could make the explosion products reassemble themselves. But a tiny inaccuracy in the motion of just one single particle, and all you would get is more junk.

Here's another example: drop a bit of black ink into a tub of water. The ink spreads out and eventually makes the water grey. Will a tub of grey water ever clear up and produce a small drop of ink? Not impossible, but very unlikely.

Boltzmann was the first to understand the statistical foundation for the second law, but he was also the first to understand the inadequacy of his own formulation. Suppose that you came upon a tub that had been filled a zillion years ago, and had not been disturbed since. You notice the odd fact that it contains a somewhat localized cloud of ink. The first thing you might ask is what will happen next. The answer is that the ink will almost certainly spread out more. But by the same token, if you ask what most likely took place a moment before, the answer would be the same: it was probably more spread out a moment ago than it is now. The most likely explanations would be that the ink-blob is just a momentary fluctuation.

Actually I don't think you would come to that conclusion at all. A much more reasonable explanation is that for reasons unknown, the tub started not-so-long-ago with a concentrated drop of ink, which then spread. Understanding why ink and water go one way becomes a problem of "initial conditions". What set up the concentration of ink in the first place?

The water and ink is an analogy for the question of why entropy increases. It increases because it is most likely that it will increase. But the equations say that it is also most likely that it increases toward the past. To understand why we have this sense of direction, one must ask the same question that Boltzmann did: Why was the entropy very small at the beginning? What created the universe in such a special low-entropy way? That's a cosmological question that we are still very uncertain about.

I began telling you what my favorite explanation is, and I ended up telling you what my favorite unsolved problem is. I apologize for not following the instructions. But that's the way of all good explanations. The better they are, the more questions they raise.

The Gaia Hypothesis

For my money, the deepest, most beautiful scientific explanation is the Gaia hypothesis, the idea that Earth's physical and biological processes are inextricably interwoven to form a self-regulating system. This notion—the 1965 brainchild of chemist James Lovelock, further co-developed with microbiologist Lynn Margulis—proposes that air (atmosphere), water (hydrosphere), earth (geosphere or pedosphere) and life (biosphere) interact to form a single evolving system capable of maintaining environmental conditions consistent with life. Lovelock initially put forth the Gaia hypothesis to explain how life on Earth has persisted for 4 billion years despite a 30% increase in the Sun's intensity over that same interval.

But how does Gaia work? Lacking a conscious command-and-control system, Lovelock and Margulis demonstrated that Gaia uses feedback loops to track and adjust key environmental parameters. Take oxygen, a highly reactive by-product of life, generated and continually replenished by photosynthetic algae and plants. The present day atmospheric concentration of oxygen is about 21%. A few percentage points lower and air-breathing life forms could not survive. A few percentage points higher and terrestrial ecosystems would become overly combustible, prone to conflagration. According to the Gaia hypothesis, oxygen-producing organisms have used feedback loops to maintain atmospheric oxygen between these narrow limits for hundreds of millions of years.

Similar arguments, backed by an ever-growing body of research, can be made for other atmospheric constituents, as well as for global surface temperature, oceanic salinity, and other key environmental metrics. Although the Gaia hypothesis highlights cooperation at the scale of the biosphere, researchers have documented multiple examples showing how cooperation at one level could evolve through competition and natural selection at lower levels. Initially criticized by serious scientists as new-age mumbo-jumbo, Lovelock's radical notion has increasingly been incorporated into scientific orthodoxy, and key elements are now often taught as "Earth Systems Science." One timely lesson resulting at least in part from Gaian research is that food web complexity, including higher species diversity, tends to enhance ecological and climate stability.

So, while Earth may inhabit a "Goldilocks zone," neither too close nor too far from the sun, life's rampant success on this "pale blue dot" cannot be ascribed to luck alone. Life has had a direct hand in ensuring its own persistence.

Science has not yet fully embraced the Gaia hypothesis. And it must be admitted that, as an explanation, this idea remains incomplete. The insights cascading from Gaia are unquestionably deep and beautiful, uniting the whole of the biosphere and Earth's surface processes into a single, emergent, self-regulating system

Yet this explanation has yet to achieve the third milestone defined in this year's Edge Annual Question—elegance. The Gaia hypothesis currently lacks the mathematical precision of Einstein's E=Mc². No unified theory of Earth and Life has been presented to explain why life stabilizes more than it destabilizes.

Evolutionary biologist W. D. Hamilton once compared Lovelock's insights to those of Copernicus, adding that we still await the Newton who will define the laws of this grand, seemingly improbable relationship. Hamilton himself became deeply engrossed in seeking an answer to this question, developing a computer model that seemed to show how stability and productivity could increase in tandem. Were it not for his untimely death, Hamilton might have emerged as that modern-day Newton, becoming, in the words of author Tim Flannery, "the most revered biologist of all time."

The cultural implications of Gaia also continue to be debated. Arguably the most profound implication of Lovelock's idea is that Earth, considered as a whole, possesses many qualities of an organism. But is Gaia actually alive, akin to a single life form, or is it more accurate to think of her as a planet-sized ecosystem? Lynn Margulis argued strongly (and convincingly, to my mind) for the latter view. Margulis, whose work revolutionized evolutionary biology at the smallest and grandest of scales, died recently. Always the hard-nosed scientist, she once said,

"Gaia is a tough bitch—a system that has worked for over three billion years without people. This planet's surface and its atmosphere and environment will continue to evolve long after people and prejudice are gone."

While not disagreeing with this blunt assessment, I find considerably greater inspiration in Gaian thinking. Indeed I would go so far as to suggest that this idea can help shift the human perception of nature. In the modernist perspective, the natural world is little more than a collection of virtually infinite resources available for human exploitation. The Gaian lens encourages us to re-envision Earth-bound nature as an intertwined, finite whole from which we evolved, and in which we remain fully embedded. Here, then, is a deep and beautiful perspective in desperate need of broad dissemination.

The Mechanism of Mediocrity

In 1969, a Canadian-born educator named Laurence J. Peter pricked the maidenhead of American capitalism. "In a hierarchy," he stated, "every employee tends to rise to his level of incompetence." He called it the Peter Principle, and it appeared in a book of the same name. The little volume, not even 180 pages long, went on to become the year's top seller, with some 200,000 copies going out bookstore doors. It's not hard to see why. Not only did the Peter Principle confirm what everyone suspected—bosses are dolts—but it explained why this had to be so. When a person excels at a job, he gets promoted. And he keeps getting promoted until he attains a job that he's not very good at. Then the promotions stop. He has found his level of incompetence. And there he stays, interminably.

The Peter Principle was a hook with many barbs. It didn't just expose the dunderhead in the corner office. It took the centerpiece of the American dream—the desire to climb the ladder of success—and revealed it to be a recipe for mass mediocrity. Enterprise was an elaborate ruse, a vector through which the incompetent made their affliction universal. But there was more. The principle had, as a New York Times reviewer put it, "cosmic implications." It wasn't long before scientists developed the "Generalized Peter Principle," which went thus: "In evolution, systems tend to develop up to the limit of their adaptive competence." Everything progresses to the point at which it founders. The shape of existence is the shape of failure.

The most memorable explanations strike us as alarmingly obvious. They take commonplace observations—things we've all experienced—and tease the hidden truth out of them. Most of us go through life bumping into trees. It takes a great explainer, like Laurence J. Peter, to tell us we're in a forest.

The Seen and the Unseen

The simple yet profound explanation of why people get themselves into serious epistemological trouble and propose idiotic policies and harebrained ideas is that they ignore the Law of Unintended Consequences. Often enough, when considering a given idea, proposal, option, or policy, people will focus only its beneficial consequences and ignore the negative or damaging ones, which may be further off in time and harder to foresee. But practically every human action entails a substantial network of consequences, and so a rational assessment of any proposal ought to take into account all of its effects, the obvious and the non-obvious, the intended and the unintended, not just those that immediately leap to the eye.

The core notion was captured most clearly by the French economist Frédéric Bastiat, who in 1850 wrote an essay called "That Which is Seen and That Which is Unseen." In it he describes a little boy's accidentally throwing a ball through a shopkeeper's window. Bystanders console the shopkeeper by telling him that, despite his loss, the accident will be a boon to the glazier, who will replace the window for six francs.  (Today this is known as "job creation.") 

True enough, the glazier benefits. "But," says Bastiat, "that is only what is seen. It is not seen that as our shopkeeper has spent six francs on one thing, he cannot spend them on another. It is not seen that if he had not had a window to replace, he would, perhaps, have replaced his old shoes, or added another book to his library. In short, he would have employed his six francs in some way, which this accident has prevented."

This so-called "parable of the broken window" has been exploited by free-market economists to oppose many ostensibly "humanitarian" government interventions that, they argue, have negative unintended consequences further down the line. Rent control, for example, while keeping some housing affordable is said to reduce the livability and availability of apartments that landlords can no longer afford to maintain. 

But the lesson of the seen and the unseen is far more encompassing in scope than its applications within the dismal science. For example, species are sometimes introduced to ecological systems with a specific, narrow purpose in mind, whereas their actual introduction is accompanied by ripple effects that go well beyond the original purpose it was intended to serve. A well-known example is the importation and breeding of cane toads in Australia in order to control the cane beetle, a pest that ravaged sugar cane crops. But not only didn't they control the cane beetle, the toads themselves soon proliferated so wildly that they became major pests in their own right, and had the further effect of converting kindly, animal-loving citizens into raging maniacs on public roads and highways on which drivers, day and night, would swerve right and left in order to run over and flatten (with a loud "pop") as many of the monsters as came into view. (In addition, a group of otherwise sane golfers placed powerful lights on golf courses to attract the toads so that they could hit them with golf clubs and propel these amphibian golf balls across the fairways to their deaths, a scheme that in any case didn’t work: "Nine times out of ten the cane toad will get up and hop away," said one unamused critic of the practice.) 

More recently, ethanol has been added to gasoline with the intention of reducing our dependence of foreign petroleum. That is what is seen. As for what is unseen, consider the set of ripple effects described by a team of energy specialists (in a 2007 piece actually entitled "The Ripple Effect: Biofuels, Food Security, and the Environment"). Since ethanol was made from corn, the increased demand for corn caused prices to rise (to wit, from $2.60 per bushel in July 2006 to $4.25 per bushel in March 2007). Higher corn prices in turn meant higher prices for corn-fed beef. It also meant that a basic food crop was made more expensive for food-insecure people who could least afford a price rise. Further ripple effects were massive increases in farmland values (making new acreage more dear to farmers), and greater use of artificial fertilizers, with increased runoffs and negative implications for nitrogen and phosphorous losses to groundwater, surface water, and the atmosphere. And so on.

Moral of the story: When entertaining the merits of some grand new miracle idea, look beyond the obvious.

Beautiful, Elegant, And … Absolutely Wrong

On April 25, 1953, in a short note to Nature entitled "Molecular structure of nucleic acids", James Watson and Francis Crick announced their deduction of the double-helix structure of DNA. Their remarkable article famously ends with one of the most laconic understatements in all of science: "It has not escaped our notice that the specific pairing we have postulated immediately suggests a possible copying mechanism for the genetic material." Indeed, the double-strands of DNA, each a mirror image of the other, explains how cells can replicate—the "secret of life" as Watson and Crick modestly announced to the startled clientele of The Eagle pub in Cambridge during a break in their labors. But the most remarkable thing about this beautiful and elegant discovery is that it is not remarkable enough to be the topic of this essay.

In fact, their structure held the key to something far more subtle and arguably of even greater fundamental importance than the mechanism for genetic replication. What Watson and Crick had uncovered was a window on the world's oldest fossil, one which sheds light not only on the static structure of modern molecular biology, but also on the dynamical processes leading to the emergence of life on Earth! The unraveling of this story is a fascinating episode in the history of science, because it involves not one, but two beautiful and elegant ideas, each of which is absolutely and unequivocally wrong! And tellingly, each beautiful but flawed idea was conceived by a physicist trying to understand biology as a jigsaw puzzle at the molecular scale. As we proceed into the second decade of this "century of biology", flooded by data but starved of fundamental insight, we will do well to resist the temptation to build biology on naïve, static principles of beauty and elegance that seemingly serve so well in the physical sciences.

Watson and Crick had shown how to pack together the four molecules ("nucleotides"—known concisely by the symbols A,C,G,T) making up DNA into a structure that fitted X-ray measurements of the atomic positions. The precise sequence of the symbols A,C,G,T somehow encoded the composition of proteins, known to be built up from a palette of twenty small molecules known as amino acids. It was the physicist George Gamow who a year later pointed out that the "key-and-lock" relation between the nucleotides of the DNA structure exhibited diamond-shaped holes, and that for geometrical reasons, these diamonds were specified by the three surrounding nucleotides. Gamow enumerated all such holes, and discovered that there were twenty different types of hole—one for each amino acid! Thus was born the idea of a "genetic code": the stupendously complicated biochemical processes going on inside every cell to make proteins could be reduced down to a simple code table, easily able to fit on a tee-shirt, that told you how to read DNA and translate its message into the proteins of living cells.

Gamow's ingenious idea for a genetic code was absolutely wrong, but serendipitously he did get right that triplets of nucleotides ("codons") code for the twenty amino acids of life. But how do they? If you write down all possible triplets of ACGT, you'll find that there are 64 (4x4x4) possible sets of three letters or codons. Evidently some of these possible codons must code for the same amino acid, or else the cell would use 64 amino acids. If the codons were doublets, then there would only be 16 (4x4) possible sets of such letters, and that would not be enough to specify each of the 20 amino acids used by life. So we are stuck with triplets, and evidently some of these triplets code for the same amino acid.

And now there are two mysteries: not only what is the code, but also, why are only 20 amino acids used by life?

These questions were answered in a brilliant article published by Crick, Griffith and Orgel in 1957. Let's follow Crick and friends, as they try to hack the genome, reverse engineering the genetic code by appealing to a logic that one might mischievously call "intelligent design". Let's suppose that we have a section of the message six characters long, some small part of the three billion characters of the human genome:

… ACGGAC …

Knowing about triplet codons, you would parse this as

ACG, GAC,

But, you say, how do we know that the first letter, the A, is actually where the message starts? Maybe the A is the last symbol in the previous codon (the … above), and the message should be parsed as

…A, CGG, AC …

with the last AC the start of the following codon. In other words, if you set out to transmit a code in this way, what would be the smart way to remove this sort of ambiguity? Crick et al. proposed that you construct the code such that it only makes sense when read with the correct starting point. In other words, you make a code in which ACG and GAC stand for meaningful symbols (in this case the amino acids Threonine and Aspartic acid), but CGG would be meaningless. Such a code can be read in only one way, so it requires no punctuation: it is what they called a "comma-less code". The beautiful discovery of Crick et al. is that the maximum number of symbols (ie. amino acids) that can be encoded in this way with triplets is twenty. And so, they concluded, Nature had been forced to work only with twenty amino acids, and not a much larger set, in order to build proteins, because it was a mathematical impossibility to construct a comma-less genetic code with more amino acids.

From their reasoning, it is not difficult to enumerate the possible comma-less genetic codes. There are 288 of them. But the actual genetic code, conclusively determined during the 1960's, is not one of them!

Beautiful, elegant, and absolutely wrong: key-and-lock mechanisms have been important in understanding snapshots of biological structure, but they are misleading clues in the search to understand the dynamical processes of evolution that have led to the phenomenon of life. Far richer than Gamow and Crick conceived, the genetic code is now thought to have been shaped rapidly over evolutionary time through the cooperative dynamics of early organisms, thus ensuring a code that is remarkably robust to errors in translation and mutations of the genome sequence. Only with such a code could such complex organisms as you and me evolve. And that is the real secret of life. 

Fact, Fiction, and Our Probabilistic World

How do we separate fact from fiction? We are frequently struck by seemingly unusual coincidences. Imagine seeing an inscription describing a fish in your morning reading, then at lunch you are served fish and the conversation turns to "April fish" (or April fools). That afternoon a work associate shows you several pictures of fish and in the evening you are presented with an embroidery of fish-like sea monsters. The next morning a colleague tells you she dreamed of fish. This might be starting to seem spooky. It actually turns out that we shouldn't find this surprising. The reason why has a long history resulting in the unintuitive insight of building randomness directly into our understanding of nature, through the probability distribution.

Chance as Ignorance

Tolstoy was skeptical of our understanding of chance. He gave an example of a flock of sheep where one had been chosen for slaughter. This one sheep was given extra food separately from the others and Tolstoy imagined that the flock, with no knowledge of what was coming, must find the continually fattening sheep extraordinary—something he thought the sheep would assign to "chance" due to their limited viewpoint. Tolstoy's solution was for the sheep to stop thinking that things happen only for "the attainment of their sheep aims" and realize that there are hidden aims that explain everything perfectly well, and so there is no need to resort to the concept of chance.

Chance as an Unseen Force

Eighty-three years later Carl Jung published a similar idea in his well-known essay "Synchronicity, An Acausal Connecting Principle." He postulated the existence of a hidden force that is responsible for the occurrence of seemingly related events that otherwise appear to have no causal connection. The initial story of the six fish encounters is Jung's, taken from his book. He finds this string of events unusual, too unusual to be ascribable to chance. He thinks something else must be going on—and labels it the acausal connecting principle.

Persi Diaconis, Stanford Professor and former professor of mine, thinks critically about Jung's example: suppose we encounter the concept of fish once a day on average according to what statisticians call a "Poisson process" (another fish reference!). The Poisson process is a standard mathematical model for counts, for example radioactive decay seems to follow a Poisson process. The model presumes a certain fixed rate at which observations appear on average and otherwise they are random. So we can consider a Poisson process for Jung's example with a long run average rate of one observation per 24 hours and calculate the probability of seeing six or more observations of fish in a 24 hour window. Diaconis finds the chance to be about 22%. Seen from this perspective, Jung shouldn't have been surprised.

The Statistical Revolution: Chance in Models of Data Generation

Only about two decades after Tolstoy penned his lines about sheep, Karl Pearson brought about a statistical revolution in scientific thinking with a new idea of how observations arose, the same idea used by Diaconis in his probability calculation above. Pearson suggested that nature presents data from an unknown distribution but with some random scatter. His insight was that this is a different concept from measurement error, which adds additional error when the observations are actually recorded.

Before Pearson, science dealt with things that were "real," such as laws describing the movement of the planets or blood flow in horses, to use examples from David Salsburg's book, The Lady Tasting Tea. What Pearson made possible was a probabilistic conception of the world. Planets didn't follow laws with exact precision, even after accounting for measurement error. The exact course of blood flow differed in different horses, but the horse circulatory system wasn't purely random. In estimating distributions rather than the phenomena themselves, we are able to abstract a more accurate picture of the world.

Chance Described by Probability Distributions

That measurements themselves have a probability distribution was a marked shift from confining randomness to the errors in the measurement. Pearson's conceptualization is useful because it permits us to estimate whether what we see is likely or not, under the assumptions of the distribution. This reasoning is now our principal tool for judging whether or not we think an explanation is likely to be true.

We can, for example, quantify the likelihood of drug effectiveness or carry out particle detection in high energy physics. Is the distribution of the mean response difference between drug treatment and control groups centered at zero? If that seems likely, we can be skeptical of the drug's effectiveness. Are candidate signals so far from the distribution for known particles that they must be from a different distribution, suggesting a new particle? Detecting the Higgs boson requires such a probabilistic understanding of the data to differentiate Higgs signals from other events. In all these cases the key is that we want to know the characteristics of the underlying distribution that generated the phenomena of interest.

Pearson's incorporation of randomness directly into the probability distribution enables us to think critically about likelihoods and quantify our confidence in particular explanations. We can better evaluate when what we see has special meaning and when it does not, permitting us to better reach our "human aims." 

Evolution By Natural Selection

My Edge answer this year has to be evolution by natural selection. Not only does it explain how we all got here and how we are and behave as we do, it can even explain (at least to my fairly critical satisfaction) why many people refuse to accept it and why even more people believe in an all-powerful Deity. But since other Edge respondents are likely to have natural selection as their favorite deep, elegant, and beautiful explanation (it has all three attributes, in addition to wide ranging explanatory power), I'll have to hone in on one particular instance: the explanation of how humans acquired language—by which I mean grammatical structure.

There is evidence to suggest that our ancestors developed effective means to communicate using verbal utterances starting at least 3 million years ago. But grammar is much more recent, perhaps as recent as 75,000 years ago. How did grammar arise?

Anyone who has traveled abroad knows that to communicate basic needs, desires, and intentions to people in your vicinity, concerning objects within sight, a few referring words, together with gestures, suffice. The only grammar required is to occasionally juxtapose two words—"Me Tarzan, you Jane" being the information- (and innuendo-) rich, classic example from Hollywood. Anthropologists refer to such a simple, word-pairing, communicative system as protolanguage.

But to communicate about things not in the immediate here-and-now, you need more. Significantly, effectively planning future joint activities needs pretty well all of grammatical structure, particularly if the planning involves more than two people, with even more demands put upon the grammar if the planned action requires coordination between different groups not all present at the same place or time.

Given the degree to which human survival depends on our ability to plan and coordinate our actions—and to collectively debrief after things go wrong so we avoid repeating our mistakes (though at a national level we seem really bad at doing that)—it is clear that grammatical structure is hugely important to Homo sapiens. Indeed, many argue that is our defining characteristic. But communication, while arguably the killer app for grammar, clearly cannot be what put it into the gene pool in the first place, and for a very simple reason. Since grammar is required in order for verbal utterances to convey more complex ideas than is possible with protolanguage, it only comes into play when the brain can form such complex ideas. These considerations lead to what I think is accepted (though not without opposition) as the "Standard Explanation" of language acquisition.

In highly simplified terms, the Standard Explanation runs like this.

1. Brains (or the organs that became brains) first evolved to associate motor responses to sensory input stimuli.

2. In some creatures, brains became more complex, performing a mediating role between input stimuli and motor responses.

3. In some of those creatures, the brain became able to over-ride what was previously an automatic stimulus-response sequence.

4. In Homo sapiens, and to a lesser extent in other species, the brain acquired the ability to function "off-line", effectively running simulations of actions without the need for sensory input stimuli and without generating output responses.

Stage 4 is when the brain acquires grammar. What we call grammatical structure is in fact a descriptive/communicative manifestation of a mental structure for modeling the world.

As a mathematician, what I like about this explanation is that it also tells us where the brain got its capacity for mathematical thinking. Namely, mathematical thinking is essentially another manifestation of the brain's simulation capacity, but in quantitative/relational/logical terms rather than descriptive/communicative.

As is usually the case with natural selection arguments, it takes considerable work to flesh out the details of these simplistic explanations, and some days I am less convinced than others about some aspects, but overall they strike me as about right. In particular, the mathematical story explains why doing mathematics carries with it an overpowering Platonistic sense of reasoning not about abstractions but real objects—at least "real" in a Platonic realm. At which point, the lifelong mathematics educator in me says I should leave the proof of that corollary as an exercise for the reader—so I shall.