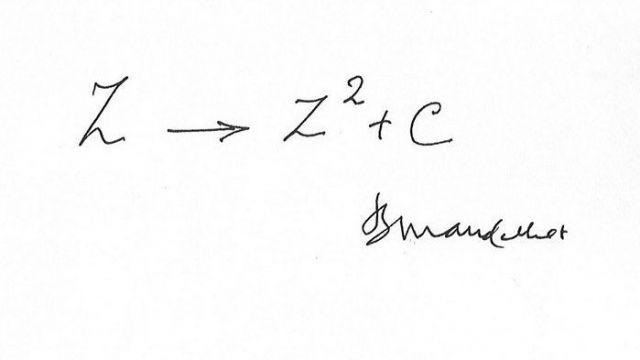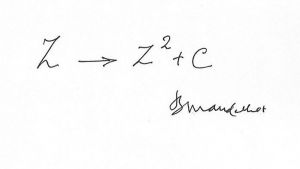My ambition was not to create a new field, but I would have welcomed a permanent group of people having interests close to mine and therefore breaking the disastrous tendency towards increasingly well-defined fields. Unfortunately, I failed on this essential point, very badly. Order doesn't come by itself. In my youth I was a student at Caltech while molecular biology was being created by Max Delbrück, so I saw what it means to create a new field. But my work did not give rise to anything like that. One reason is my personality — I don't seek power and do not run around. A second is circumstances — I was in an industrial laboratory because academia found me unsuitable. Besides, creating close organized links between activities which otherwise are very separate might have been beyond any single person's ability.
That issue is important to me now, in terms of legacy. Let me elaborate. When I turned seventy, a former postdoc organized a festive meeting in Curaçao. It was superb because of the participation of mathematician friends, physicist friends, engineering friends, economist friends and many others. Geographically, Curaçao is out of the way, hence not everybody could make it, but every field was represented. Several such meetings had been organized since 1982. However, my enjoyment of Curaçao was affected by a very strong feeling that this was going to be the last such common meeting. My efforts over the years had been successful to the extent, to take an example, that fractals made many mathematicians learn a lot about physics, biology, and economics. Unfortunately, most were beginning to feel they had learned enough to last for the rest of their lives. They remained mathematicians, had been changed by considering the new problems I raised, but largely went their own way.
Today, various activities united at Curaçao are again quite separate. Notable exceptions persist, to which I shall return in a moment. However, as I was nearing eighty, a Curaçao-like meeting was not considered at all. Instead, the event is being celebrated by more than half a dozen specialized meetings in diverse locations. The most novel and most encouraging one will be limited to very practical applications of fractals, to issues concerning plastics, concrete, the internet, and the like.
For many years I had been hearing the comment that fractals make beautiful pictures, but are pretty useless. I was irritated because important applications always take some time to be revealed. For fractals, it turned out that we didn't have to wait very long. In pure science, fads come and go. To influence basic big-budget industry takes longer, but hopefully also lasts longer.
To return to and explain how fractals have influenced pure mathematics, let me say that I am about to spend several weeks at the Mittag-Leffler Instituteat the Swedish Academy of Sciences. Only 25 years ago, I had no reason to set foot there, except to visit the spectacular library. But, as it turned out, my work has inspired three apparently distinct programs at this Institute.
~~
The first was held in the 1980s when the Mandelbrot Set was a topic of a whole year of discussion. It may not be widely appreciated that the discovery of that set had consisted in empowering the eye again, in inspecting pictures beyond counting and on their basis stating a number of observations and conjectures to which I drew the mathematicians' attention. One of my conjectures was solved in six months, a second in five years, a third in ten. But the basic conjecture, despite heroic efforts rewarded by two Fields Medals, remains a conjecture, now called MLC: the Mandelbrot Set is locally connected. The notion that these conjectures might have been reached by pure thought — with no picture — is simply inconceivable.
The next Mittag-Leffler year I inspired came six years ago and focused on my "4/3" conjecture about Brownian motion. Its discovery is characteristic of my research style and my legacy, hence deserves to be retold.
Scientists have known Brownian motion for centuries, and the mathematical model provided by Norbert Wiener is a marvelous pillar at the very center of probability theory. Early on, scientists had made pictures both of Brownian motion in nature and of Wiener's model. But this area developed like many others in mathematics and lost all contact with the real world.
My attitude has been totally different. I always saw a close kinship between the needs of "pure" mathematics and a certain hero of Greek mythology, Antaeus. The son of Earth, he had to touch the ground every so often in order to reestablish contact with his Mother; otherwise his strength waned. To strangle him, Hercules simply held him off the ground. Back to mathematics. Separation from any down-to-earth input could safely be complete for long periods — but not forever. In particular, the mathematical study of Brownian motion deserved a fresh contact with reality.
Seeking such a contact, I had my programmer draw a very big sample motion and proceeded to play with it. I was not trying to implement any preconceived idea, simply actively "fishing" for new things. For a long time, nothing new came up. Then I conceived an idea that was less scientific than esthetic. I became bothered by the fact that, when a Brownian motion has been drawn from time 0 to time 1, its two end portions and its middle portion follow different rules. That is, the whole is not homogeneous, exhibits a certain lack of inner symmetry, a deficit of beauty.
This triggered the philosophical prejudice that when you seek some unspecified and hidden property, you don't want extraneous complexity to interfere. In order to achieve homogeneity, I decided to make the motion end where it had started. The resulting motion biting its own tail created a distinctive new shape I call Brownian cluster. Next the same purely aesthetic consideration led to further processing. The continuing wish to eliminate extraneous complexity made me combine all the points that cannot be reached from infinity without crossing the Brownian cluster. Painting them in black sufficed, once again, to create something quite new, resembling an island. Instantly, it became apparent that its boundary deserved to be investigated. Just as instantly, my long previous experience with the coastlines of actual islands on Earth came handy and made me suspect that the boundary of Brownian motion has a fractal dimension equal to 4/3. The fractal dimension is a concept that used to belong to well-hidden mathematical esoteric. But in the previous decades I had tamed it into becoming an intrinsic qualitative measure of roughness.
Empirical measurement yielded 1.3336 and on this basis, my 1982 book, The Fractal Geometry of Nature, conjectured that the value of 4/3 is exact. Mathematician friends chided me: had I told them before publishing, they could have quickly provided a fully rigorous proof of my conjecture. They were wildly overoptimistic, and a proof turned out to be extraordinarily elusive. A colleague provided a numerical approximation that fitted 4/3 to about 15 decimal places, but an actual proof took 18 years and the joining of contributions of three very different scientists. It was an enormous sensation in the year 2000. Not only the difficult proof created its own very active sub field of mathematics, but it affected other, far removed, sub fields by automatically settling many seemingly unrelated conjectures. An article in Science magazine reported to my great delight a comment made at a major presentation of the results, that this was the most exciting thing in probability theory in 20 years. Amazing things started happening and the Mittag-Leffler Institute organized a full year to discuss what to do next.
Today, after the fact, the boundary of Brownian motion might be billed as a "natural" concept. But yesterday this concept had not occurred to anyone. And even if it had been reached by pure thought, how could anyone have proceeded to the dimension 4/3? To bring this topic to life it was necessary for the Antaeus of Mathematics to be compelled to touch his Mother Earth, if only for one fleeting moment.
Within the mathematical community, the MLC and 4/3 conjectures had a profound effect — witnessed recently when the French research council, CNRS, expressed itself as follows. "Mathematics operates in two complementary ways. In the 'visual' one the meaning of a theorem is perceived instantly on a geometric figure. The 'written' one leans on language, on algebra; it operates in time. Hermann Well wrote that 'the angel of geometry and the devil of algebra share the stage, illustrating the difficulties of both.'"
I, who took leave from French mathematics at age 20 because of its rage against images, could not have described it better. Great to be alive when these words come from that pen. But don't forget that, in the generations between Hermann Well (1885-1955) and today — the generations of my middle years — the mood had been totally different.
Back to cluster dimension. At IBM, where I was working at the time, my friends went on from the Brownian to other clusters. They began with the critical percolation cluster, which is a famous mathematical structure of great interest in statistical physics. For it, an intrinsic complication is that the boundary can be defined in two distinct ways, yielding 4/3, again, and 7/4. Both values were first obtained numerically but by now have been proven theoretically, not by isolated arguments serving no other purpose, but in a way that has been found very useful elsewhere. As this has continued, an enormous range of geometric shapes, so far discussed physically but not rigorously, became attractive in pure mathematics, and the proofs were found to be very difficult and very interesting.
The third meeting that my work inspired at the Mittag-Leffler Institute of the Swedish Academy, will take place this year. Its primarily concern will be a topic I have already mentioned, the mathematics of the Internet.
This may or may not have happened to you, but some non-negligible proportion of e/mail gets lost. Multiple identical messages are a pest, but the sender is actually playing it safe for the good reason that in engineering everything is finite. There is a very complicated way in which messages get together, separate, and are sorted. Although computer memory is no longer expensive, there's always a finite size buffer somewhere. When a big piece of news arrives, everybody sends a message to everybody else, and the buffer fills. If so, what happens to the messages? They're gone, just flow into the river.
At first the experts thought they could use an old theory that had been developed in the 1920s for telephone networks. But as the Internet expanded, it was found that this model won't work. Next they tried one of my inventions from the mid-1960s, and it wouldn't work either. Then they tried multi fractals, a mathematical construction that I had introduced in the late 1960s and into the 1970s. Multi fractals are the sort of concept that might have been originated by mathematicians for the pleasure of doing mathematics, but in fact it originated in my study of turbulence and I immediately extended it to finance. To test new internet equipment one examines its performance under multi fractal variability. This is even a fairly big business, from what I understand.
~~
How could it be that the same technique applies to the Internet, the weather and the stock market? Why, without particularly trying, am I touching so many different aspects of many different things?
A recent, important turn in my life occurred when I realized that something that I have long been stating in footnotes should be put on the marquee. I have engaged myself, without realizing it, in undertaking a theory of roughness. Think of color, pitch, heaviness, and hotness. Each is the topic of a branch of physics. Chemistry is filled with acids, sugars, and alcohols; all are concepts derived from sensory perceptions. Roughness is just as important as all those other raw sensations, but was not studied for its own sake.
In 1982 a metallurgist approached me, with the impression that fractal dimension might provide at long last a measure of the roughness of such things as fractures in metals. Experiments confirmed this hunch, and we wrote a paper for Nature in 1984. It brought a big following and actually created a field concerned with the measurement of roughness. Recently, I have moved the contents of that paper to page 1 of every description of my life's work.
Those descriptions have repeatedly changed, because I was not particularly precocious, but I'm particularly long-lived and continue to evolve even today. Above a multitude of specialized considerations, I see the bulk of my work as having been directed towards a single overarching goal: to develop a rigorous analysis for roughness. At long last, this theme has given powerful cohesion to my life. Earlier on, since my Ph.D. thesis in 1952, the cohesion had been far more flimsy. It had been based on scaling, that is, on the central role taken by so-called power-law relations.
For better or worse, none of my acquaintances has or had a similar story to tell. Everybody I have known has been constantly conscious of working in a pre-existing field or in one being consciously established. As a notable example, Max Delbrück was first a physicist, and then became the founder of molecular biology, a field he always understood as extending the field of biology. To the contrary, my fate has been that what I undertook was fully understood only after the fact, very late in my life.
To appreciate the nature of fractals, recall Galileo's splendid manifesto that "Philosophy is written in the language of mathematics and its characters are triangles, circles and other geometric figures, without which one wanders about in a dark labyrinth." Observe that circles, ellipses, and parabolas are very smooth shapes and that a triangle has a small number of points of irregularity. Galileo was absolutely right to assert that in science those shapes are necessary. But they have turned out not to be sufficient, "merely" because most of the world is of infinitely great roughness and complexity. However, the infinite sea of complexity includes two islands: one of Euclidean simplicity, and also a second of relative simplicity in which roughness is present, but is the same at all scales.
The standard example is the cauliflower. One glance shows that it's made of florets. A single floret, examined after you cut everything else, looks like a small cauliflower. If you strip that floret of everything except one "floret of a floret" — very soon you must take out your magnifying glass — it's again a cauliflower. A cauliflower shows how an object can be made of many parts, each of which is like a whole, but smaller. Many plants are like that. A cloud is made of billows upon billows upon billows that look like clouds. As you come closer to a cloud you don't get something smooth but irregularities at a smaller scale.
Smooth shapes are very rare in the wild but extremely important in the ivory tower and the factory, and besides were my love when I was a young man. Cauliflowers exemplify a second area of great simplicity, that of shapes which appear more or less the same as you look at them up close or from far away, as you zoom in and zoom out.
Before my work, those shapes had no use, hence no word was needed to denote them. My work created such a need and I coined "fractals." I had studied Latin as a youngster, and was trying to convey the idea of a broken stone, something irregular and fragmented. Latin is a very concrete language, and my son's Latin dictionary confirmed that a stone that was hit and made irregular and broken up, is described in Latin by the adjective "fractus." This adjective made me coin the word fractal, which now is in every dictionary and encyclopedia. It denotes shapes that are the same from close and far away.
~~
Do I claim that everything that is not smooth is fractal? That fractals suffice to solve every problem of science? Not in the least. What I'm asserting very strongly is that, when some real thing is found to be un smooth, the next mathematical model to try is fractal or multi fractal. A complicated phenomenon need not be fractal, but finding that a phenomenon is "not even fractal" is bad news, because so far nobody has invested anywhere near my effort in identifying and creating new techniques valid beyond fractals. Since roughness is everywhere, fractals — although they do not apply to everything — are present everywhere. And very often the same techniques apply in areas that, by every other account except geometric structure, are separate.
To give an example, let me return to the stock market and the weather. It's almost trite to compare them and speak of storms and hurricanes on Wall Street. For a while the market is almost flat, and almost nothing happens. But every so often it hits a little storm, or a hurricane. These are words which practical people use very freely but one may have viewed them as idle metaphors. It turns out, however, that the techniques I developed for studying turbulence — like weather — also apply to the stock market. Qualitative properties like the overall behavior of prices, and many quantitative properties as well, can be obtained by using fractals or multi fractals at an extraordinarily small cost in assumptions.
This does not mean that the weather and the financial markets have identical causes — absolutely not. When the weather changes and hurricanes hit, nobody believes that the laws of physics have changed. Similarly, I don't believe that when the stock market goes into terrible gyrations its rules have changed. It's the same stock market with the same mechanisms and the same people.
A good side effect of the idea of roughness is that it dissipates the surprise, the irritation, and the unease about the possibility of applying fractal geometry so widely.
The fact that it is not going to lack problems anytime soon is comforting. By way of background, a branch of physics that I was working in for many years has lately become much less active. Many problems have been solved and others are so difficult that nobody knows what to do about them. This means that I do much less physics today than 15 years ago. By contrast, fractal tools have plenty to do. There is a joke that your hammer will always find nails to hit. I find that perfectly acceptable. The hammer I crafted is the first effective tool for all kinds of roughness and nobody will deny that there is at last some roughness everywhere.
I did not and don't plan any general theory of roughness, because I prefer to work from the bottom up and not from top to bottom. But the problems are there. Again, I didn't try very hard to create a field. But now, long after the fact, I enjoy this enormous unity and emphasize it in every recent publication.
The goal to push the envelope further has brought another amazing development, which could have been described as something recent, but isn't. My book, The Fractal Geometry of Nature, reproduced Hokusai's print of the Great Wave, the famous picture with Mt. Fuji in the background, and also mentioned other unrecognized examples of fractality in art and engineering. Initially, I viewed them as amusing but not essential. But I changed my mind as innumerable readers made me aware of something strange. They made me look around and recognize fractals in the works of artists since time immemorial. I now collect such works. An extraordinary amount of arrogance is present in any claim of having been the first in "inventing" something. It's an arrogance that some enjoy, and others do not. Now I reach beyond arrogance when I proclaim that fractals had been pictured forever but their true role remained unrecognized and waited for me to be uncovered.

Photo: Marvin Minsky

Initial image of a Mandelbrot set zoom sequence with a continuously coloured environment

Benoit Mandelbrot, Budapest, 16 October 2003 [Photo: George Dyson]

FORMULA FOR THE 21ST CENTURY [10.13.07] WHAT IS YOUR FORMULA? YOUR EQUATION? YOUR ALGORITHM?