Many mathematical surveys indicate that the "Proof of the Riemann Hypothesis" is the most important open question in mathematics. The rapid pace of mathematics, along with computer-assisted mathematical proofs and visualizations, leads me to believe that this question will be resolved in my lifetime. Math aficionado John Fry once said that he thought we would have a better chance of finding life on Mars than finding a counterexample for the Riemann Hypothesis.
In the early 1900s, British mathematician Godfrey Harold Hardy sometimes took out a quirky form of life insurance when embarking on ocean voyages. In particular, he would mail a postcard to a colleague on which he would claim to have found the solution of the Riemann Hypothesis. Hardy was never on good terms with God and felt that God would not let him die in a sinking ship while Hardy was in such a revered state, with the world always wondering if he had really solved the famous problem.
The proof of the Riemann Hypothesis involves the zeta function, which can be represented by a complicated-looking curve that is useful in number theory for investigating properties of prime numbers. Written as f(x), the function was originally defined as the infinite sum:
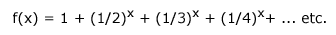
When x = 1, this series has no finite sum. For values of x larger than 1, the series adds up to a finite number. If x is less than 1, the sum is again infinite. The complete zeta function, studied and discussed in the literature, is a more complicated function that is equivalent to this series for values of x greater than 1, but it has finite values for any real or complex number, except for when the real part is equal to one. We know that the function equals zero when x is -2, -4, -6, ... . We also know that the function has an infinite number of zero values for the set of complex numbers, the real part of which is between zero and one—but we do not know exactly for what complex numbers these zeros occur. In 1859, mathematician Georg Bernhard Riemann (1826–1866) conjectured that these zeros occur for those complex numbers the real part of which equals 1/2. Although vast numerical evidence exists that favors this conjecture, it is still unproven
The proof of Riemann's Hypothesis will have profound consequences for the theory of prime numbers and in our understanding of the properties of complex numbers. A generalized version of the Hypothesis, when proven true, will allow mathematicians to solve numerous important mathematical problems. Amazingly, physicists may have found a mysterious connection between quantum physics and number theory through investigations of the Riemann Hypothesis. I do not know if God is a mathematician, but mathematics is the loom upon which God weaves the fabric of the universe.
Today, over 11,000 volunteers around the world are working on the Riemann Hypothesis, using a distributed computer software package at Zetagrid.Net to search for the zeros of the Riemann zeta function. More than 1 billion zeros for the zeta function are calculated every day.
In modern times, mathematics has permeated every field of scientific endeavor and plays an invaluable role in biology, physics, chemistry, economics, sociology, and engineering. Mathematics can be used to help explain the colors of a sunset or the architecture of our brains. Mathematics helps us build supersonic aircraft and roller coasters, simulate the flow of Earth's natural resources, explore subatomic quantum realities, and image faraway galaxies. Mathematics has changed the way we look at the cosmos.
Physicist Paul Dirac once noted that the abstract mathematics we study now gives us a glimpse of physics in the future. In fact, his equations predicted the existence of antimatter, which was subsequently discovered. Similarly, mathematician Nikolai Lobachevsky said that "there is no branch of mathematics, however abstract, which may not someday be applied to the phenomena of the real world."

















